Комбинаторика на ММО: графы, турниры, логика, конструктивы
Ошибка.
Попробуйте повторить позже
У Полины есть колода из карт (
масти по
карт в каждой). Она выбирает из неё половину карт, какие хочет, и отдает Василисе, а
вторую половину оставляет себе. Далее каждым ходом игроки по очереди открывают по одной карте по своему выбору (соперник видит
масть и достоинство открытой карты), начиная с Полины. Если в ответ на ход Полины Василиса смогла положить карту той же масти или
того же достоинства, то Василиса зарабатывает одно очко. Какое наибольшее количество очков Василиса может гарантированно
заработать?
Источники:
Подсказка 1
Какие карты должна взять себе Полина, чтобы Василиса гарантированно не смогла подобрать пару?
Подсказка 2
Чтобы не получилось подобрать карту, у Василисы не должно оказаться карты ни той же масти, ни того же достоинства. Для скольки карт получится это сделать?
Подсказка 3
Получится ли у Василисы подобрать оставшийся максимум пар карт в любом случае?
Подсказка 4
У нас есть 9 групп по 4, и они же 4 группы по 9. Как было бы удобно их расположить для лучшего и более наглядного оценивания пар Полина-Василиса?
Подсказка 5
Да, можно нарисовать таблицу 4х9, разделив карты по масти и достоинству. А что обычно лучше всего делать с таблицей?
Подсказка 6
Давайте сделаем раскраску, где закрашенные — карты Полины, а незакрашенные — карты Василисы. И если пару можно составить только из карт разного цвета в одном столбике или строчке, то сколько таких пар гарантированно сможет составить Василиса?
Подсказка 7
Поскольку в одном столбике меньше карт, чем в одной строке, стоит разбить табличку именно на них. Какую характеристику было бы удобно дать каждому из столбиков? И на какие пары стоит разбить столбики в связи с этой характеристикой?
Подсказка 8
4 и 0 дают 4 пары, 3 и 1 тоже. 2 прекрасны сами по себе. То есть по сколько пар дает каждый столбик, если поделить? Какие столбики могут остаться?
Подсказка 9
Остались 4 или 0 и 3 или 1. Сколько таких столбцов может остаться?
Подсказка 10
Вспомним, что белых и чёрных клеток суммарно поровну, тогда как связаны количества белых и чёрных клеток, если убрать все "парные" столбики, рассмотренные ранее?
Подсказка 11
Из равенства количества белых и черных получаем связь между количеством "одиночных" столбцов, что дает возможность разбить их на группы. Сколько пар гарантированно будет в каждой такой группе? А сколько максимум будет таких групп а значит, и "потерь" пар?
Если Полина возьмёт себе все черви, все тузы, всех королей и всех дам, то Василиса не сможет набрать очки на тузе, короле и даме червей,
т. е. наберёт не больше очков.
Теперь докажем, что при любом выборе Полины Василиса может заработать не меньше очков. Выложим карты в клетки таблицы
(в одном столбце карты одного достоинства, в одной строке — карты одной масти). Докажем, что если Полина закрасила черным
клеток, то Василиса может выделить не менее
непересекающихся xороших пар: в каждой паре две клетки разного цвета, находящиеся в
одной строке или одном столбце. (Тогда Василиса на ход одной картой из пары сможет отвечать ходом второй карты из этой пары и
заработать
очков.)
Назовём типом столбца количество чёрных клеток в нём. Сначала Василиса рассматривает столбцы типа (если они есть). Каждый из
них, очевидно, разбивается на две хорошие пары.
Далее Василиса рассматривает пары столбцов типа и
Каждая такая пара, очевидно, разбивается на четыре хорошие пары
клеток.
Далее Василиса рассматривает пары столбцов типа и
Каждая такая пара тоже разбивается на четыре хорошие пары клеток (см.
рисунок слева).
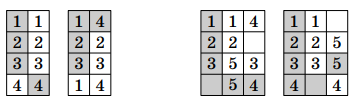
Когда указанные пары столбцов закончатся, в силу симметрии можно считать, что “необработанными” останутся только
столбцы типов и
Если это
столбцов типа
и
столбцов типа
то
т. е.
В тройке из
столбца типа
и двух столбцов типа
Василиса сможет выделить не менее пяти хороших пар клеток (см. рисунок
справа).
Так как то на всей доске останется не более трёх нехороших пар, т. е. Василиса «потеряет» не больше
очков.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




