Комбинаторика на ММО: графы, турниры, логика, конструктивы
Ошибка.
Попробуйте повторить позже
Из шахматной доски вырезали
клеток. Известно, что среди вырезанных клеток есть как черные, так и белые. Какое наибольшее
количество двухклеточных прямоугольников можно после этого гарантированно вырезать из этой доски?
Источники:
Подсказка 1
Заметьте, что каждый двухклеточный прямоугольник содержит разноцветные клетки. Какую оценку тогда можно сделать?
Подсказка 2
Если мы вырежем 9 белых и 1 черную клетки, то получим не более 32 - 9 = 23 прямоугольников. А давайте сначала разрежем доску на прямоугольники, и только потом уже будет удалять клетки.
Подсказка 3
Мы вырезаем 10 клеток, следовательно, будет испорчено не более 10 прямоугольников. Значит, у нас есть по крайней мере 22 прямоугольника. Попробуем увеличить это количество. Возможно, нам в этом может помочь какая-то цепочка, идущая по прямоугольникам.
Подсказка 4
Разрежем доску следующим образом: в первой строке у нас будут прямоугольники a8-b8, c8-d8 и так далее. В нижней строке аналогично. С остальными клетками поступим так: на линии "a" будут прямоугольники a7-a6, a5-a4, a3-a2. С остальными линиями аналогично. Какую цепочку можно пустить по этим прямоугольникам?
Подсказка 5
Она будет стартовать в клетке a2, идти вверх до a8, потом в клетку b8, далее в b7, идти вниз до клетки b2, далее в c2 и снова наверх. В нижней строке она пойдет справа-налево и вернется до a2. Что можно сказать про клетки, расположенные на пути этой цепочки?
Подсказка 6
Мы вырезаем белые и черные клетки, следовательно, за некоторой вырезанной белой клеткой будет идти вырезанная черная клетка. Попробуйте подумать про взаимное расположение этих двух клеток.
Подсказка 7
Если эти две клетки соседние, то при некотором разрезании они испортят только один прямоугольник, следовательно, будет не менее 23 целых прямоугольников. А что, если эти клетки не соседние?
Подсказка 8
Попробуйте по-другому разрезать клетки между ними и вновь получить 23 прямоугольника.
Каждый двухклеточный прямоугольник содержит чёрную и белую клетки, поэтому если вырезано 9 белых клеток, то больше
прямоугольников вырезать не получится.
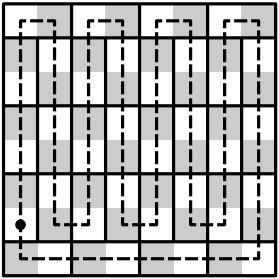
Разрежем доску так, как показано на рис. 1. Вырезанные из доски клетки при разрезании “испортят” не более 10 прямоугольников. Следовательно, у нас уже есть по крайней мере 22 целых прямоугольника. Покажем, как увеличить количество целых прямоугольников на 1. Рассмотрим изображённую на рис. 1 замкнутую цепочку клеток (по цепи идём от клетки а2 вверх). Поскольку вырезаны как белые, так и чёрные клетки, в этой цепи обязательно есть вырезанная белая клетка, за которой идёт вырезанная чёрная клетка.
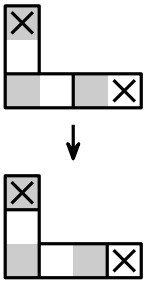
Если эти клетки соседние, то они “портят” только один прямоугольник, значит, при таком разрезании будет не менее 23 целых прямоугольников.
В противном случае, если между ними есть ещё клетки, разделим доску между ними так, чтобы новый прямоугольник начинался сразу после вырезанной белой клетки (см. рис. 2). Тогда количество целых прямоугольников увеличится на 1. Следовательно, опять будет не менее 23 целых прямоугольников.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




