Стереометрия на Курчатове
Ошибка.
Попробуйте повторить позже
Пусть — правильная четырёхугольная пирамида с основанием
На отрезке
нашлась точка
такая, что
и плоскости
и
перпендикулярны. Найдите отношение
.
Источники:
Подсказка 1
У нас точка M равноудалена от точек A и B. Быть может, попробуем найти ещё такие точки? Какое дополнительное построение может помочь найти все такие точки?
Подсказка 2
Постройте сечение плоскостью, являющейся серединным перпендикуляром к SB. Заодно и середину R у SB отметим, вдруг пригодится;) Какие точки и прямые туда попадут?
Подсказка 3
Именно, AC полностью лежит в построенной плоскости! Значит, теперь нам удобно работать со многими интересными треугольниками, которые лежат в этой же плоскости. Нам нужно найти некоторое отношение на AC, никаких длин нам не дано, поэтому имеем право обозначить AO за 1. Какие тогда отрезки мы можем посчитать?
Подсказка 4
AO = SO = 1, а OR — медиана в прямоугольном треугольнике, значит, можем посчитать и её ;) а что ещё можно сказать про R? в каких плоскостях она лежит, что примечательного есть в них?
Подсказка 5
RM перпендикулярна плоскости (SAB)! Тогда у нас возникли ещё прямоугольные треугольники, в которых также можно посчитать отрезки ;)
Обозначим центр основания за
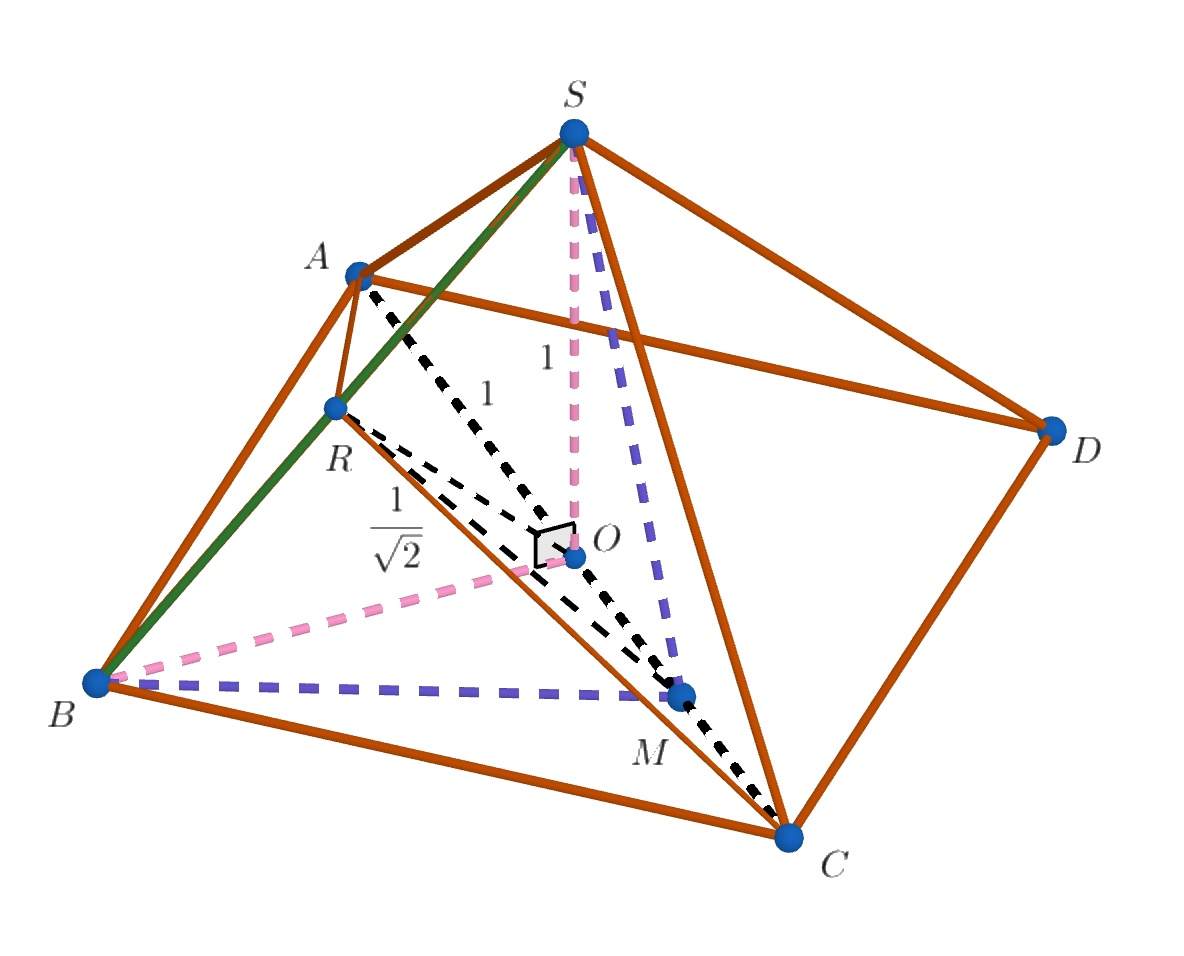
Тогда и
откуда
Это означает, что серединный перпендикуляр к отрезку
(это плоскость,
обозначим её за
) параллелен
С другой стороны, из
следует, что точка
лежит в
Тогда и вся прямая
должна содержаться в
Отсюда получаем
Середину обозначим за
. Заметим, что
лежит сразу в двух плоскостях, перпендикулярных
:
и
Это
означает, что
и сам перпендикулярен плоскости
а также отрезку
Примем длину за
Тогда
является медианой в прямоугольном равнобедренном треугольнике
; так как катеты этого треугольника равны по
имеем
.
Наконец, рассмотрим сечение тетраэдра плоскостью
Треугольник прямоугольный, причём
в нём — высота к гипотенузе. Имеем
, то есть
,
откуда
. Получаем
и
.
Замечание.
Утверждение о том, что боковое ребро пирамиды перпендикулярно скрещивающейся с ним диагонали, считается очевидным; за отсутствие его доказательства баллы не снижаются.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




