Планиметрия на ПВГ
Ошибка.
Попробуйте повторить позже
Квадрат со стороной
и квадрат
со стороной
имеют общую вершину
при этом точка
лежит на отрезке
Найдите наибольшее и наименьшее возможные значения площади параллелограмма
если точка
лежит на отрезке
и
делит его в отношении
Источники:
Подсказка 1
Каждый раз, когда мы делаем картинку к задаче, следует задаться вопросом: а единственная ли эта картинка? Не допускает ли условие того, что точки могут располагаться по-разному? Подумайте, сколько случаев есть в данной задаче.
Подсказка 2
Верно, есть два варианта: когда точка F лежит вне большого квадрата и когда она лежит внутри него. Рассмотрим для начала первый случай. Какие интересные вещи мы можем вспомнить про площадь параллелограмма?
Подсказка 3
В голову может прийти конструкция рельсов Евклида, позволяющая сравнивать площади треугольников, ограниченных параллельными прямыми. Например, чему равна площадь треугольника ACF?
Подсказка 4
Во-первых, его площадь равна половине площади искомого параллелограмма. А во-вторых, она равна площади треугольника ACD! Какой тогда можно сделать вывод о площади параллелограмма?
Подсказка 5
Да, эта площадь постоянна и равна половине площади большого квадрата! Супер, с одним из случаев разобрались, теперь рассмотрим второй! Тут так же площадь треугольника ACF равна половине площади параллелограмма. А что насчёт отношения площадей треугольников ACF и ACD?
Подсказка 6
Эти треугольники имеют общее основание, поэтому их площади относятся так же, как и их высоты! Осталось найти отношение высот и задача решена!
Возможны две разные конфигурации, в зависимости от того, где лежит точка вне большого квадрата или внутри него.
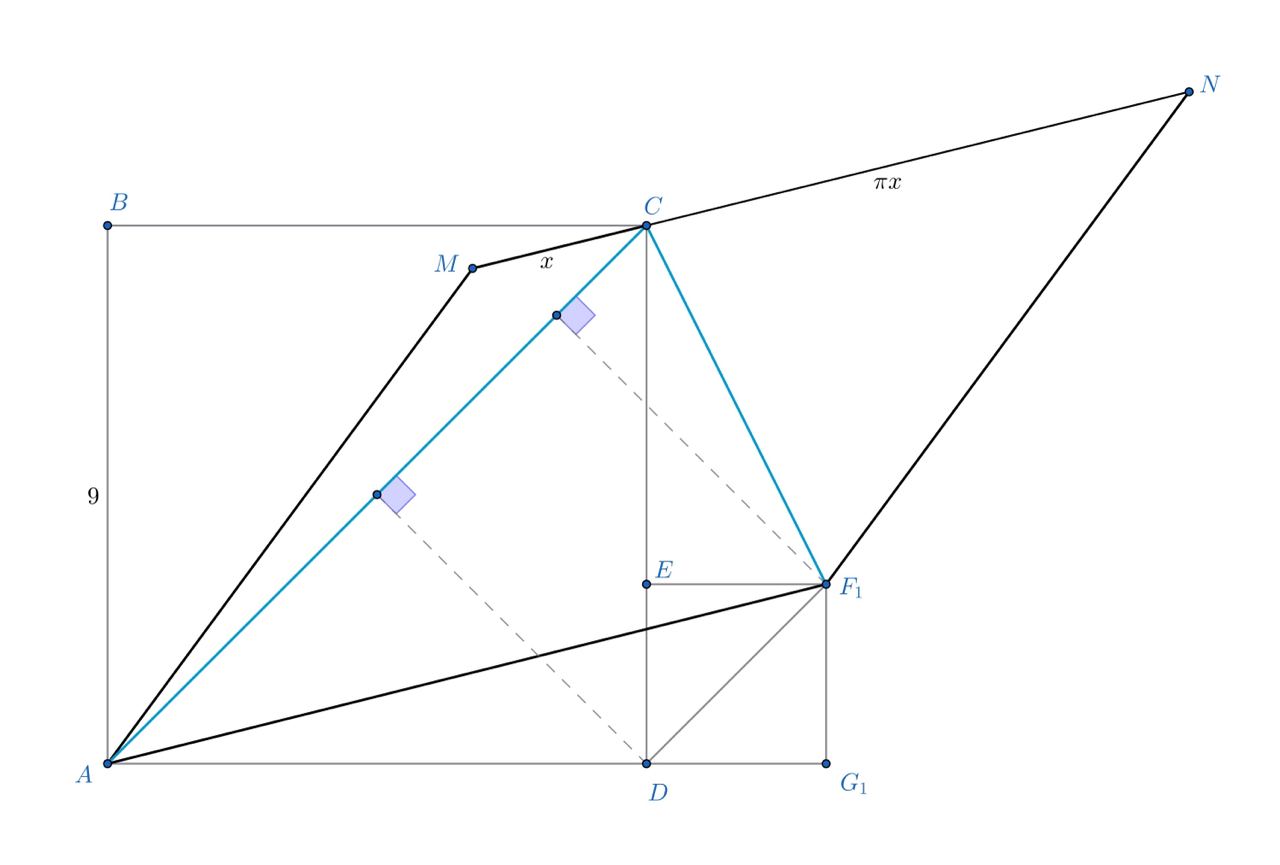
В случае внешнего касания квадратов площадь равна площади
(эти треугольники имеют одинаковое основание
и
равные высоты, так как
) и, следовательно, равна половине площади большого квадрата. Это значит, что площадь
параллелограмма равна площади квадрата
то есть
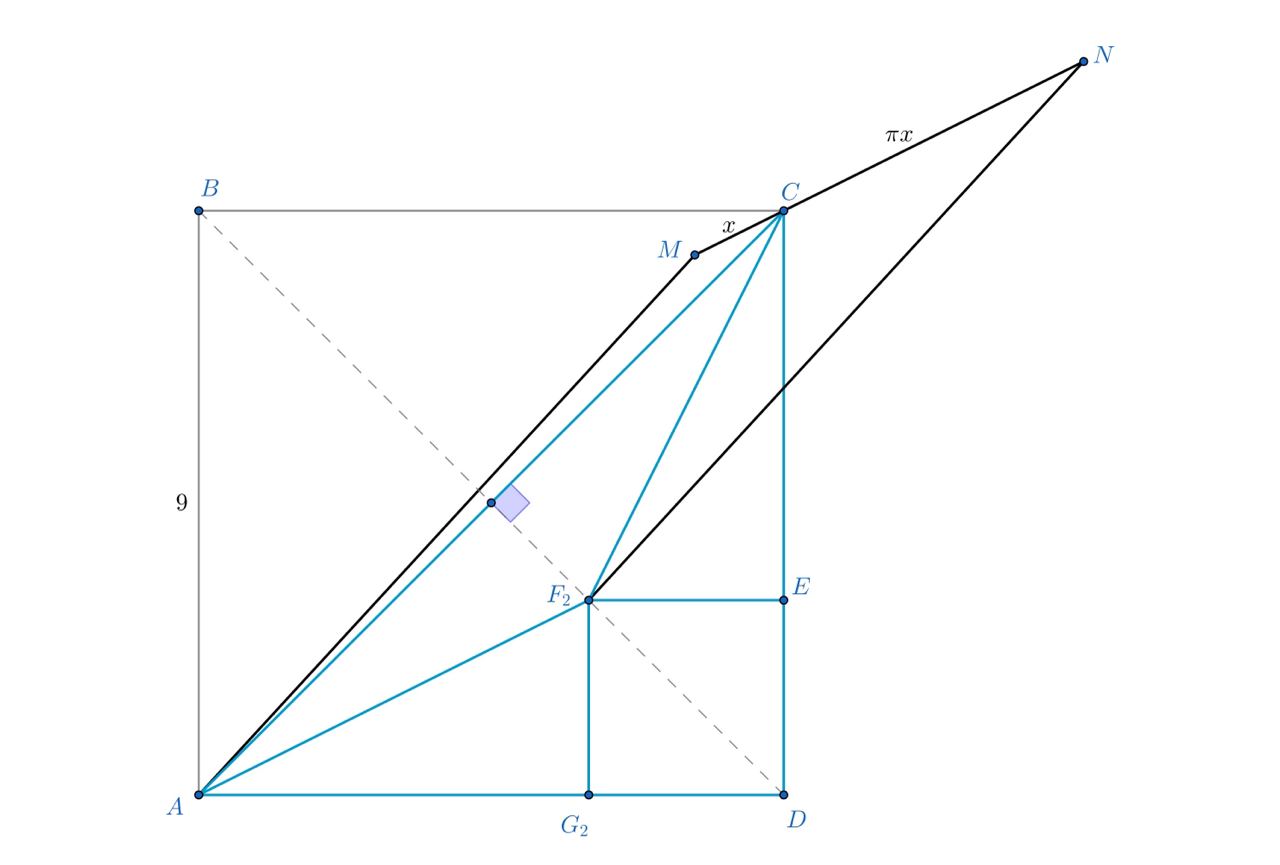
Рассмотрим случай, когда точка лежит внутри большого квадрата. Найдем отношение высот треугольников
и
(основания у них одинаковы) — оно равно
Тогда искомая площадь равна
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




