Планиметрия на ПВГ
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике на высоте
, равной основанию
, как на диаметре построена окружность, пересекающая
боковую сторону
в точке
. Каково отношение площади треугольника
к площади треугольника
Какая часть площади
треугольника
находится внутри окружности?
Источники:
Подсказка 1!
Давайте обозначит CF за x и попробуем посмотреть, что у нас получается. Основание треугольника обозначим за 2a. Давайте обозначим еще оснаток BF за y. Мы знаем, что трегуольник BFH прямоугольный, тогда давайте воспользуемся теоремой о соотношении катетов в прямоугольном треугольнике! Попробуйте найти отношение y/x.
Подсказка 2!
Да, записав теорему мы получим, что это соотношение равно 4. Осталось только найти соотношение площадей)
Подсказка 3!
Так, займемся пунктом b. Было бы здорово попробовать избавиться от x и выразить его через a. Для нахождения площади сегментов окружности, нам придется обратиться к цглам и центру. Отметьте центр окружности и заметим, что тогда в треугольнике BOF можно написать теорему косинусов! Остается аккуратно посчитать и ответить на вопрос.
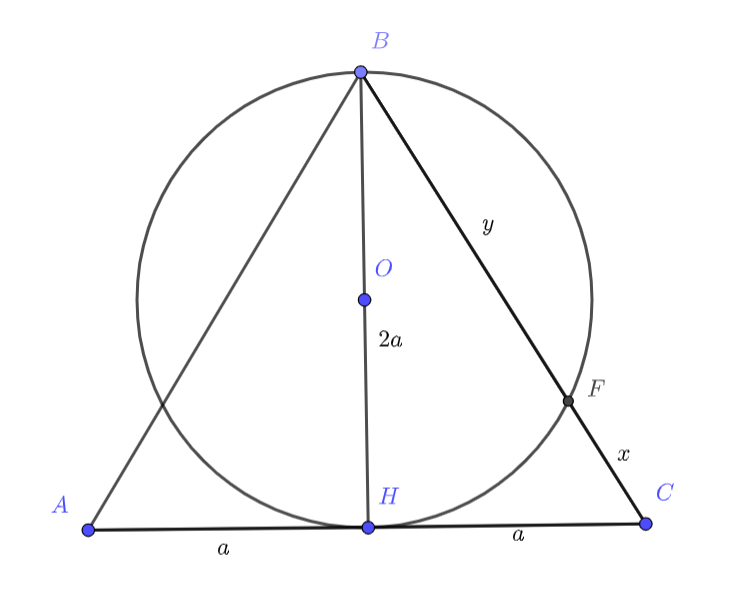
Введем обозначения: . Поскольку угол
- прямой, то по теореме об соотношениях в прямоугольном
треугольнике для двух катетов
будем иметь:
Из отношения площадей треугольников с общим углом находим ответ на первый вопрос:
Из теоремы Пифагора для имеем
. Далее пусть
— центр окружности из условия, а также
, запишем теорему косинусов для
Обозначим площадь сектора через
. Тогда
. Внутри окружности у треугольника два таких сектора. Кроме
того, внутри окружности два треугольника одинаковой площади (симметрия относительно
). Найдем площадь
. Тогда ответ на второй вопрос будет следующий:
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




