Планиметрия на ПВГ
Ошибка.
Попробуйте повторить позже
Среди всех вписанных четырёхугольников найдите четырёхугольник 
с наименьшим периметром, в котором 
и все
попарные расстояния между точками 
, 
и 
выражаются целыми числами. Чему при этом равен радиус описанной вокруг
окружности?
Источники:
Так как хорды 
и 
равны, то равны и дуги 
и 
а значит, равны вписанные углы 
и 
Это означает, что
, и 
— трапеция с равными боковыми сторонами 
и 
. Пусть 
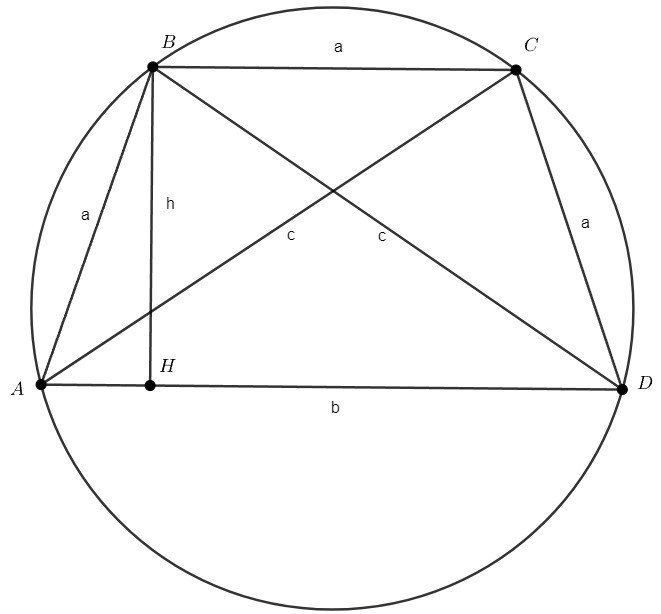
Высоту 
выразим по теореме Пифагора
Заметим, что это же можно было получить с помощью теоремы Птолемея:
Таким образом,
где 
— натуральные числа. Кроме того, 
то есть 
- Если
то ![b∈[1;2],](/api/latex-service/v1/GetSession/131604/index-d5500fbe8ca22f10e11b299af20db99c.svg)
и уравнение 
целых решений не имеет.
- Если
то ![b∈[1;5],](/api/latex-service/v1/GetSession/131604/index-0aa824c29b0626ee52ed73aed76b5f2c.svg)
и уравнение 
целых решений не имеет.
- Если
то ![b∈[1;8],](/api/latex-service/v1/GetSession/131604/index-a162eee43ef68d2bec7256b8b15de717.svg)
и уравнение 
целых решений не имеет.
- Если
то ![b∈ [1;11],](/api/latex-service/v1/GetSession/131604/index-24ca05662f87c582229f510370336e50.svg)
и уравнение 
имеет единственное целое решение 
Тогда периметр
равен 
- При
периметр будет больше 17, так как если 
то 
Но тогда или 
или
— то и другое невозможно.
Итак, 
периметр равен 17. Тогда высота трапеции равна 
синус угла
при основании равен 
а искомый радиус находится по теореме синусов
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
