Планиметрия на Ломоносове
Ошибка.
Попробуйте повторить позже
Из равнобедренного треугольника с углом 
при вершине и площадью 1 вырезают максимальный по площади круг, а из него —
максимальный по площади треугольник, подобный исходному. Какое наибольшее и наименьшее значение принимает площадь 
полученного в итоге треугольника при 
Источники:
Подсказка 1
Для начала поймём, что это за треугольники и окружности — очевидно, что это соотвественно вписанная окружность и вписанный в нее треугольник (иначе, мы могли бы увеличить площадь, дополнив до вписанной/ого). Значит, площадь вырезанного треугольника легко считается и выражается через наши параметры — площадь начального и угол. Однако нужно ли нам выражать? Просто ли так нам дали площадь большого?
Подсказка 2
Конечно, не просто так. Нам можно получить лишь отношение сторон и найти отношение площадей как коэффициент подобия в квадрате. Поэтому, найдя отношение сторон, мы сможем его промаксимизировать. Но через что выразить? Через стороны большого треугольника долго и некрасиво, а вот через радиус и угол - более чем! Подумайте лишь над тем, всегда ли одинаково все выражается.
Подсказка 3
При разных alpha размер стороны вырезанного треугольника выражается одинаково, вот только угол будет разный в зависимости от того, тупой ли треугольник, но синус остается неизменным. Осталось понять, как нам максимизировать функцию отношения… Но ведь она монотонна!
Пусть дан треугольник 
— это середина 
Заметим, что максимальный по площади круг лежащий в данном треугольник
является кругом, ограниченный вписанной окружностью. Пусть 
— центр вписанной окружности, 
и 
— радиус окружности.
Тогда половина основания можно вычислить из подобия 
и 
Так как вырезаемый треугольник 
подобный исходному 
лежит внутри фиксированной окружности, то у него по
крайней мере две вершины лежат на окружности, в противном случаи мы сможем увеличить площадь. Дальше рассмотрим два варианта:
-
Исходный треугольник
остроугольный или прямоугольный, то есть тогда 
Тогда треугольник 
будет вписан в
вырезанную окружность. 
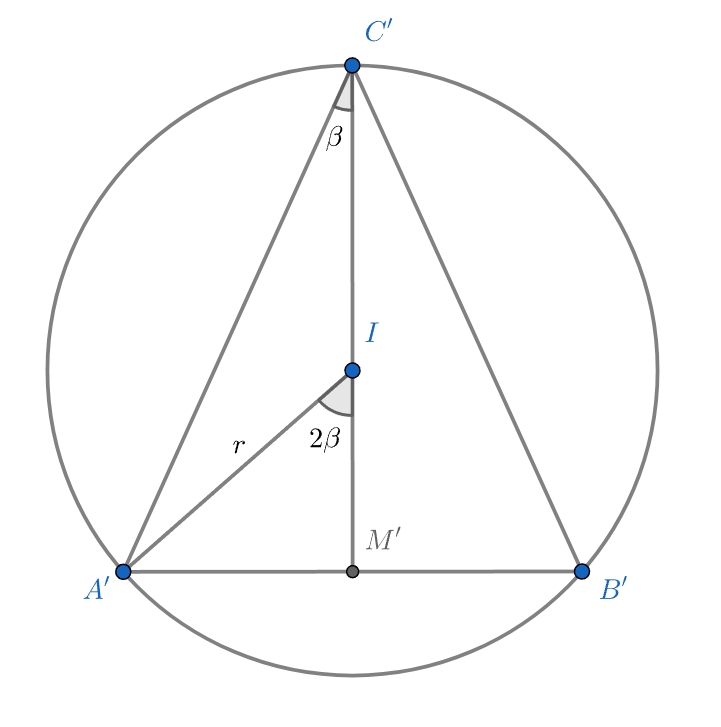
В этом случаи половина основания вырезанного треугольника равна
-
Исходный треугольник
тупоугольным, то есть тогда 
Тогда треугольник 
будет расположен так, что 
будет диаметром вырезанной окружности. 
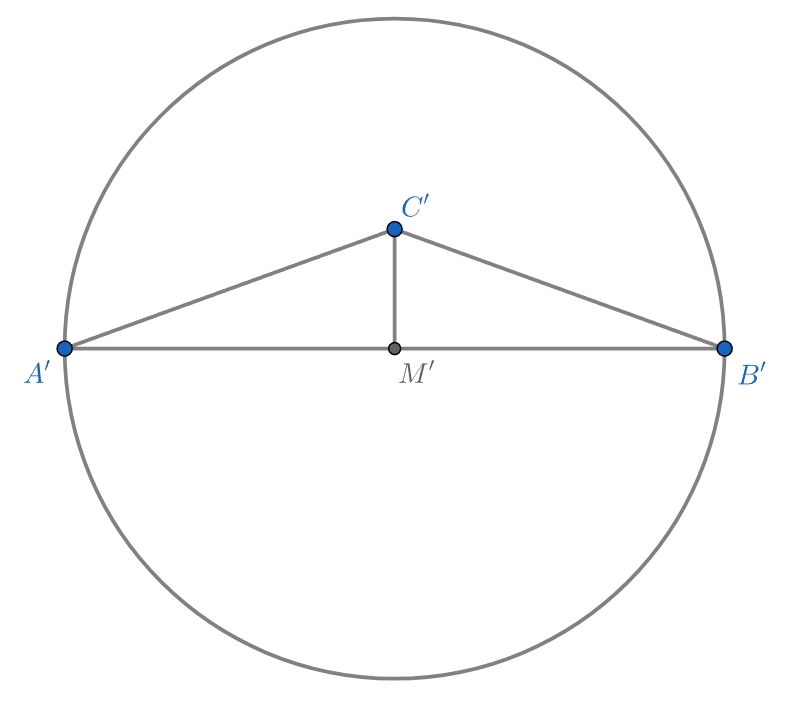
В этом случаи половина основания вырезанного треугольника равна
В итоге получаем
Тогда коэффициент подобия будет равен
В силу подобия 
и 
и того, что площадь исходного треугольника была равна 1, получаем, что
Функция убывает при ![α∈ [60∘;120∘],](/api/latex-service/v1/GetSession/184241/index-27ed4dc42eb99bf72097bb66c240d787.svg)
то есть ![β ∈ [30∘,60∘],](/api/latex-service/v1/GetSession/184241/index-aadde0818ba9b841e2411193513f1d80.svg)
поэтому
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
