Теория чисел на СПБГУ: десятичная запись, оценка+пример, разные системы счисления
Ошибка.
Попробуйте повторить позже
На картинке нарисовано несколько кружочков, соединённых отрезками.
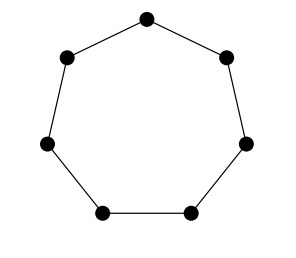
Саша выбирает натуральное число и расставляет в кружочках различные натуральные числа так, чтобы для всех этих чисел
выполнялось свойство: если числа
и
не соединены отрезком, то сумма
должна быть взаимно проста с
a если соединены, то
числа
и
должны иметь общий натуральный делитель, больший 1.
При каком наименьшем существует такая расстановка?
Источники:
Подсказка 1
Чтобы как-то снизить количество вариантов для n, давайте подумаем: а может ли n быть чётным?
Подсказка 2
Нет, поскольку если n чётно, то по принципу Дирихле найдутся два числа одинаковой чётности, которые не будет соединены! А значит их сумма кратна 2, поэтому НОД не будет равен 1. А теперь, зададимся вопросом: а могут ли три суммы четырех последовательно соединенных чисел быть кратны одному и тому же делителю числа n?
Подсказка 3
Нет, ведь в таком случае сумма крайних чисел(которые не соединены ребром) - тоже будет кратна этому делителю! То есть, число n не может равняться степени нечётного простого, поэтому оно кратно хотя бы двум различным нечётным простым! Теперь мы хотим взять минимальные простые(дли минимальности n), то есть, надо узнать, а может ли n быть кратно 3?
Подсказка 4
И опять-таки нет, n не может быть кратно 3. Поскольку, в таком случае найдётся пара чисел, соединенных ребром, сумма которых не будет кратна 3(для этого достаточно рассмотреть остатки при делении 3) То есть тройки не может быть среди простых! Осталось проверить, можно ли составить пример для n=5*7.
Сделаем два замечания.
1) нечетно. Действительно, пусть
четно. Среди семи чисел всегда есть три числа одной четности, и по условию они должны быть
попарно соединены. Но на картинке нет циклов длины 3.
2) Если — простой делитель
то среди четырех последовательно соединенных чисел существует пара соседних, сумма которых не
кратна
Возьмем цепочку
последовательно соединенных чисел. По условию
Тогда числа и
тоже соединены, то есть на картинке получился цикл длины 4, которого там нет.
Из 1) и 2) вытекает, что число имеет по крайней мере два различных нечетных простых делителя. Пусть их ровно два (скажем,
и
Покажем, что они отличны от 3. Допустим, например, что
Не более двух чисел делятся на 3 (если их три, то они образуют
цикл). Остальные числа разобьем на две группы, дающие при делении на 3 остатки 1 и 2. Одна из этих групп пуста, иначе любое число из
меньшей группы будет соединено по крайней мере с тремя числами из другой группы, что невозможно. Сумма чисел из одной группы на 3
не делится. Поэтому существует трехзвенная цепочка, в которой сумма любой пары соединенных чисел не кратна 3 и, значит, делится на
Но это противоречит 2).
Таким образом, если имеет ровно два различных нечетных простых делителя, то
Если же таких делителей больше
двух, то
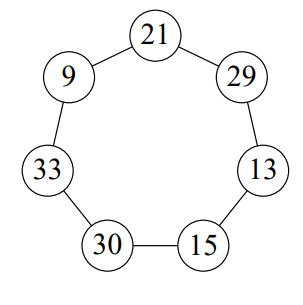
. Расстановка для
приведена на рисунке.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




