Планиметрия на СПБГУ
Ошибка.
Попробуйте повторить позже
Пусть и
— две такие окружности с центрами
и
соответственно, что окружность
проходит через точку
На окружности
вне окружности
выбрана точка
Касательные к
проходящие через
касаются
в точках
и
и вторично
пересекают
в точках
и
Отрезки
и
пересекаются в точке
Докажите, что прямые
и
перпендикулярны.
Источники:
Подсказка 1
Одна окружность проходит через центр другой не просто так. Пользуйтесь этим. Чем является прямая OM в угле AMB? А что можно сказать про отрезки CO, OD и точки C, D?
Подсказка 2
Итак, предлагается следующая идея. Давайте обозначим точку пересечения CD и OP через E' и докажем, что она лежит на AB.
Подсказка 3
Для реализации подсказки 2 нужно просто немного посчитать углы. С этим вам поможет вписанный четырёхугольник ACE'O.
Для начала заметим, что поскольку и
— касательные к окружности
а точка
— центр
то
Значит,
т. е. дуги
и
окружности
равны, т. е. точки
и
симметричны относительно прямой
Пусть — точка пересечения прямых
и
В силу симметрии
и
мы знаем, что
Докажем, что
Для этого достаточно проверить, что
лежит на прямой
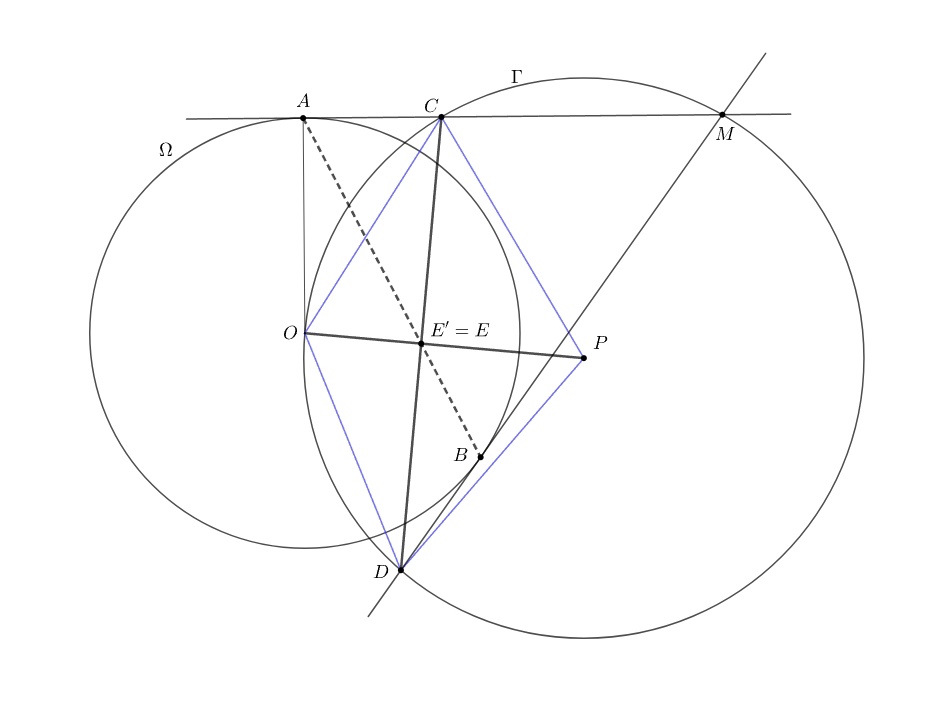
Пусть Вписанный угол в два раза меньше центрального, поэтому
Поскольку из равнобедренного треугольника
получаем, что
Далее, в четырёхугольнике
известно, что
(первое равенство — угол между радиусом и касательной, второе равенство доказано выше), поэтому
этот четырёхугольник вписанный и
где второе равенство следует из симметрии точек и
а третье — из того, что вписанный угол в два раза меньше центрального,
опирающегося на ту же дугу. Итак, точка
лежит на том же луче, выходящем из точки
что и точка
поэтому
лежит на
откуда
что и требовалось.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




