Планиметрия на СПБГУ
Ошибка.
Попробуйте повторить позже
Диагонали вписанного четырехугольника 
пересекаются в точке 
Внутри треугольника 
выбрана такая точка 
что
прямая 
является биссектрисой угла 
Луч 
вторично пересекает описанную окружность треугольника 
в точке 
а
луч 
вторично пересекает описанную окружность треугольника 
в точке 
Найдите отношение площадей треугольников
и 
Источники:
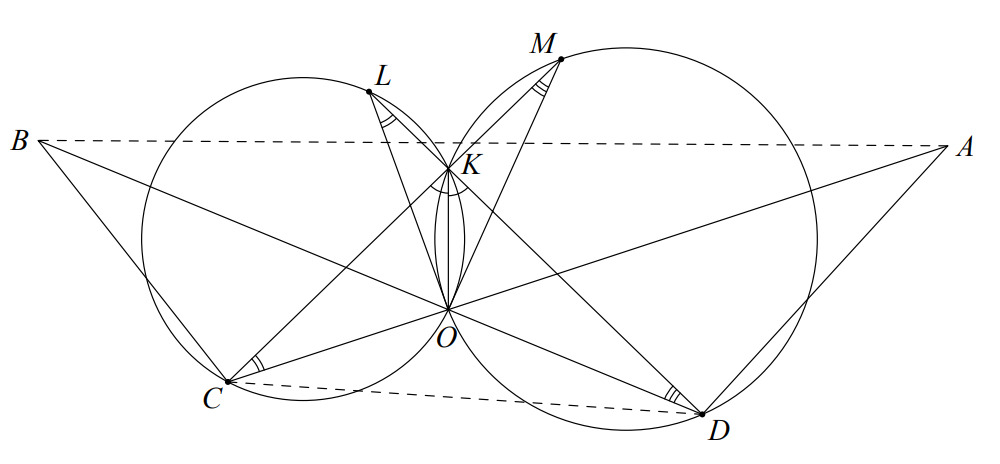
Пусть 
и 
— радиусы окружностей, описанных около треугольников 
и 
соответственно. Заметим, что
откуда 
. Кроме того, из вписанности 
вытекает, что треугольники 
и 
подобны по двум углам.
Тогда
так как хорды 
и 
соответствуют одинаковым вписанным углам. Поэтому
Поскольку 
и 
треугольники 
и 
подобны, откуда
Таким образом,
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
