Стереометрия на Росатоме
Ошибка.
Попробуйте повторить позже
Через четыре точки попарные расстояния между которыми равны
проведена сфера
Через точки
и
расположенные на ребрах
и
пирамиды
соответственно, проведена прямая, пересекающая сферу в точках
и
(
лежит между
и
). Известно, что точки
и
делят хорду
в отношении
Найти длину отрезка
Источники:
Подсказка 1
Из условия тетраэдр ABCD правильный, нам будет удобно отметить у него середины рёбер, про которые нам что-то известно (рёбра AB и CD). Попробуйте посчитать какие-нибудь отрезки на картинке!
Подсказка 2
Здесь можно применить теорему о произведении отрезков секущей: CF × FD = MF × FN, а также AE × EB = ME × EN. Для удобно введём обозначения длин отрезков PE и QF и ME. Попробуйте записать выше указанные равенства с помощью этих обозначний.
Подсказка 3
Если внимательно посмотреть на картинку, на ней можно заметить много прямоугольных треугольников :) Да, воспользовавшись теоремой о трёх перпендикулярах можно сделать вывод, что △PQE, △EQF и △QFP прямоугольные, а это значит, что можно применить теорему Пифагора! Здесь мы сможем получить ещё одно соотношение на ранее введённые параметры.
Подсказка 4
Теперь осталось собрать в кучу все полученные равенства. Хм, не замечаете ничего странного? Все ли они согласованы между собой?
Из условия понятно, что — правильный тетраэдр. Попарные расстояния между точками
обозначим через
Введем обозначения: — середины ребер
и
Пусть
— длины отрезков
и
а длины отрезков
соответственно равны
и
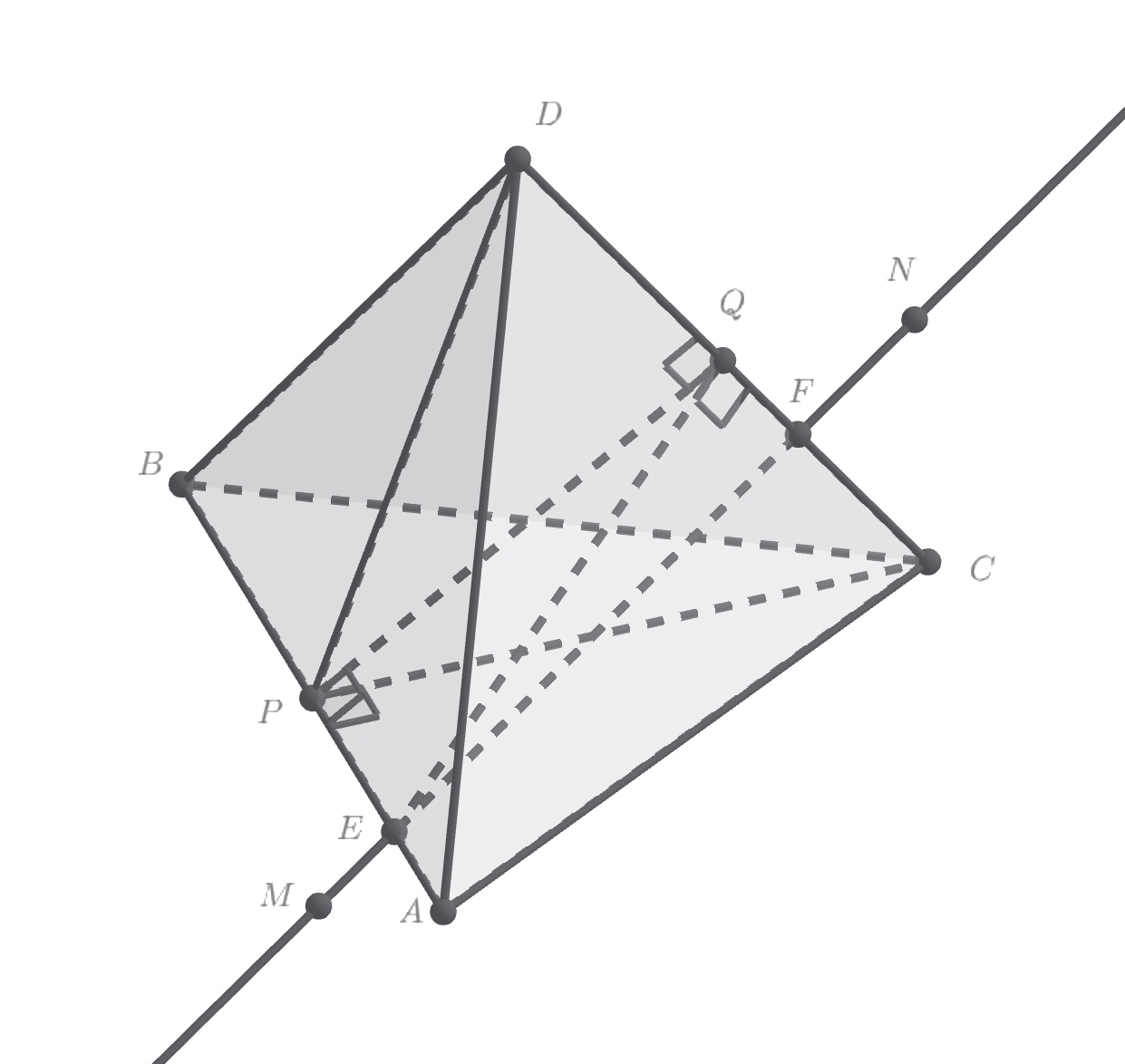
Треугольник — равнобедренный и
— его медиана, перпендикулярная
Тогда
Плоскость треугольника перпендикулярна
поэтому
и
— пересекающиеся хорды сферы,
поэтому
| (1) |
и
– пересекающиеся хорды сферы, поэтому
| (2) |
Складывая и
получим
| (3) |
Треугольники и
прямоугольные (теорема о трёх перпендикулярах), поэтому
| (4) |
Используя то, что квадрат величины неотрицательное число и равенства и
получаем:
Таким образом, должно выполняться что невозможно, так как
Значит, указанное отношение длин невозможно.
Точки и
не могут делить хорду
в заданном отношении.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




