Стереометрия на Росатоме

Введем декартову систему координат с началом координат в точке ось направим вдоль ось — на плоскости основания перпендикулярно оси абсцисс и ось перпендикулярно плоскости основания.

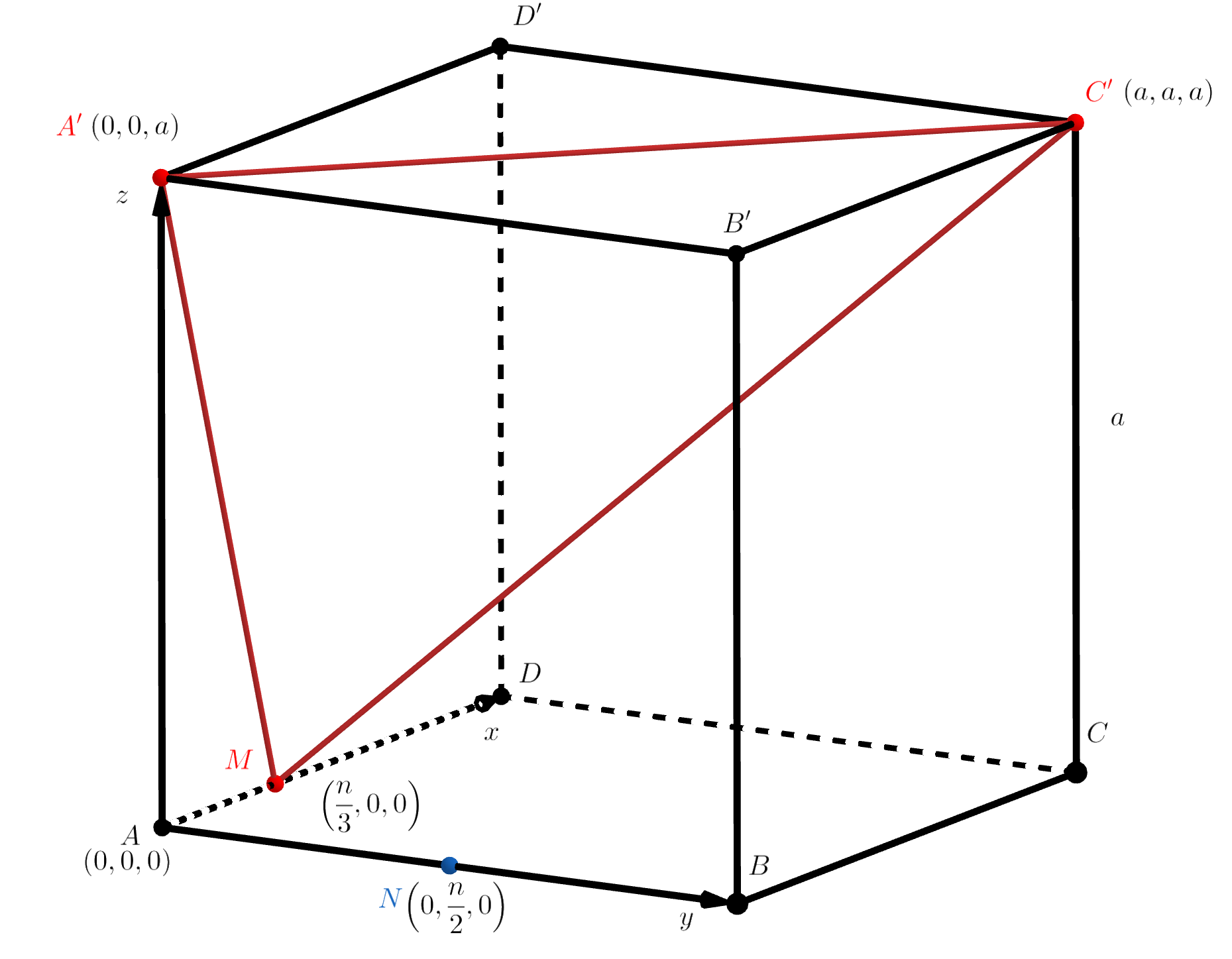
Обозначим ребро куба через отношения

Выписываем координаты нужных нам точек:

Находим уравнение плоскости в виде подставив координаты точек При этом так как плоскость не проходит через начало координат, то без ограничения общности можно считать, что

Получим систему:

Откуда получаем, что

Находим расстояние от точки до плоскости по формуле

где — координаты точки

Получим