Параметры на Росатоме
Ошибка.
Попробуйте повторить позже
При каких 
уравнение 
имеет единственное решение?
Источники:
Подсказка 1
Внимательно посмотрим на левую часть. С аркфункциями работать не хочется, поэтому нужно от них избавиться. Нам намного удобнее работать с выражением arccos(cos(x)). Попробуйте привести всё к нему в левой части.
Подсказка 2
Отлично! Левая часть равна π/2 - arccos(cos(x)). Теперь взглянем на правую часть. Тут также хочется избавиться от тригонометрических функций. Обозначьте arcsin(x - a) как за угол α и воспользуйтесь тем, что sin(α) = x - a.
Подсказка 3
Так, теперь мы получили, что левая часть равна √(1 - (x-a)^2). Попробуем изобразить графики полученных функций.(Заметьте, что левую часть можно рассматривать только на отрезке [-π;π], ведь у неё период 2π).
Подсказка 4
Нам нужно только одно решение. То есть можно смотреть только на a от -π до π, а потом записать ответ с периодом 2π. Теперь всего лишь осталось посмотреть, как наша полуокружность движется в зависимости от a, и найти точки, где одно пересечение.
Изобразим график 
на ![[−π,π]](/api/latex-service/v1/GetSession/93010/index-a209af39a26f5fe5806459c5a012eb48.svg)
. Сама функция имеет период 
, поэтому на остальной прямой график будет повторяться
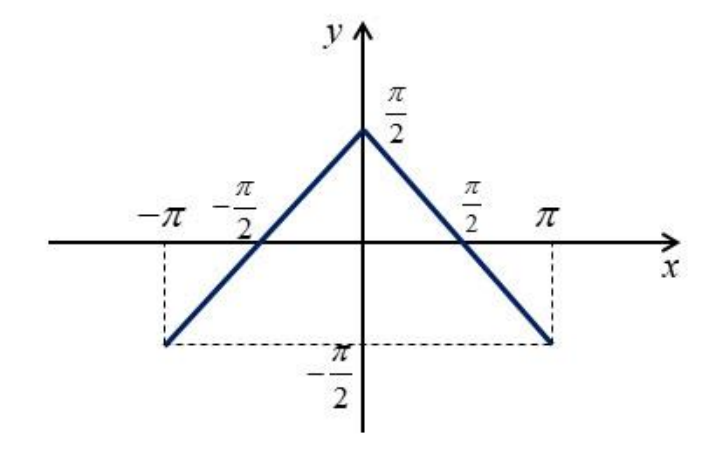
Теперь посмотрим на график правой части 
, который будет полуокружностью
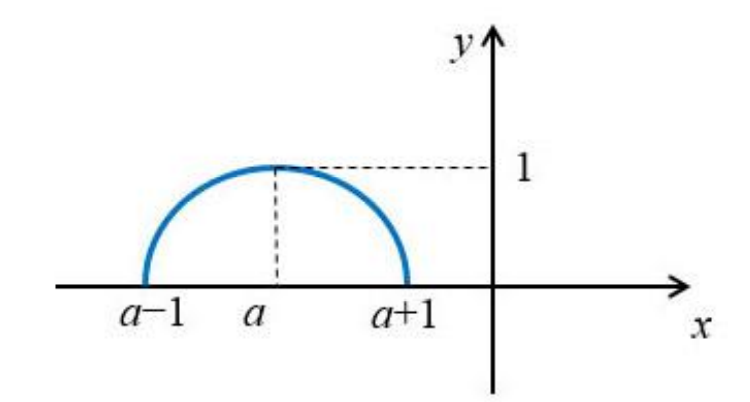
Например, графики будут расположены так при 
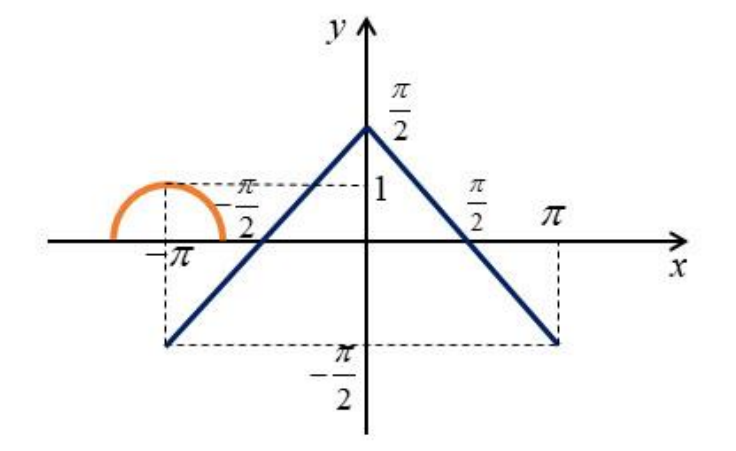
С ростом параметра 
оранжевый график перемещается вправо. Достаточно рассмотреть значения ![a ∈[−π,π]](/api/latex-service/v1/GetSession/93010/index-9c62d40227ab70c00c4a4bf17a024333.svg)
, поскольку оранжевый
график может пересекать не более одного “уголка” синего графика (помним про периодичность). Остаётся найти те значения параметра,
при которых изменяется количество общих точек на ![[−π,π]](/api/latex-service/v1/GetSession/93010/index-b07fc73dfdf292419b5c22acbc292f9b.svg)
.
Первое такое значение будет в момент первого пересечения при движении оранжевого графика вправо
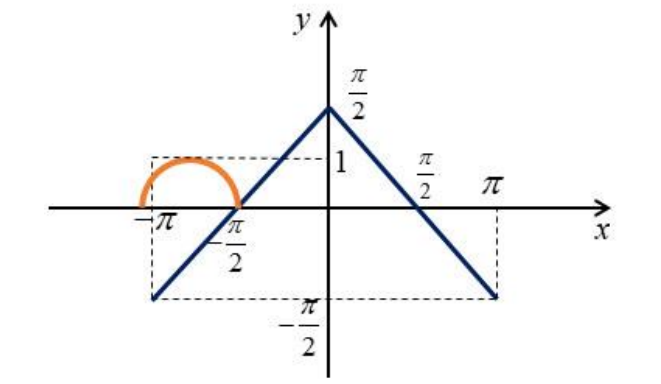
Заметим, что правая точка оранжевого графика соответствует 
, откуда
При дальнейшем движении решение будет только одно вплоть до положения
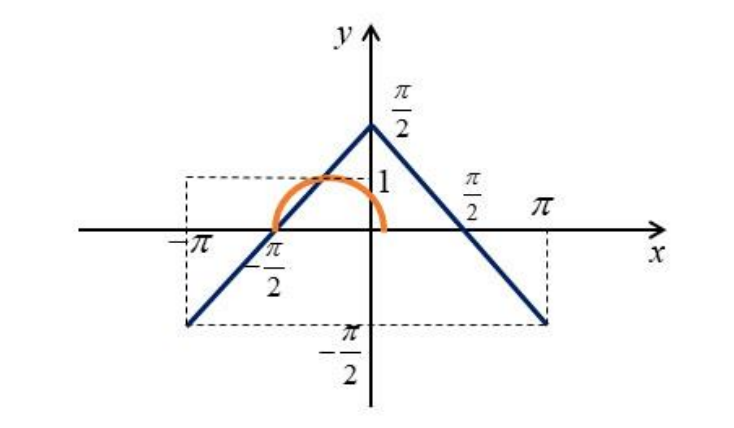
когда решений становится два. Левая точка оранжевого графика соответствует 
, откуда
Дальше решения будет два вплоть до положения, когда произойдёт касание
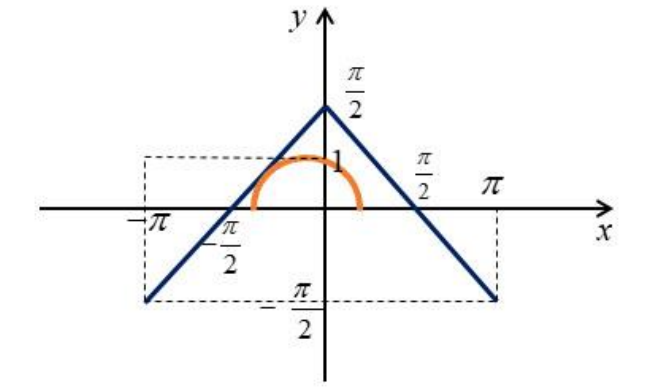
Поскольку касательная имеет коэффициент наклона 
, то на полуокружности это точка 
(учитывая смещение на 
из
центра координат). При этом точка касания лежит на прямой 
(левая часть уголка), откуда
Далее решений не будет вплоть до касания с противоположной стороны уголка в симметричной точке 
, где решение
будет одно. Далее вплоть до 
решений два. Потом от неё до 
решение единственное, а после до 
решений нет.
В итоге для единственности подойдут
![a ∈[a1,a2)∪(a5,a6]∪{a3,a4}](/api/latex-service/v1/GetSession/93010/index-8ca2eff071c1dfed3db10112c81206f0.svg)
Остаётся учесть период и написать ответ.
![[− π− 1+ 2πk,− π + 1+2πk)∪ (π − 1+2πk,π+ 1+ 2πk]∪{− π+ √2+ 2πk,π − √2-+ 2πk} , k∈ ℤ
2 2 2 2 2 2](/api/latex-service/v1/GetSession/93011/index-a0b57f591f4873e25e23aac4049ce5c2.svg)
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
