Комбинаторика и комбигео на ФЕ
Ошибка.
Попробуйте повторить позже
Маша нарисовала на клетчатой бумаге по линиям сетки квадрат 
клеток, где 
чётное число. В некоторых клетках она провела
диагонали, соблюдая два правила: - нельзя проводить две диагонали в одной клетке; - нельзя проводить две диагонали с общим
концом.
Какое наименьшее число пустых клеток могло остаться на Машином рисунке?
Источники:
Оценка. Разобьём квадрат 
на 
горизонтальных прямоугольников 
. Докажем, что в каждом из них Маша может провести
не более 
отрезка, соблюдая условие задачи. Для каждого такого прямоугольника отметим все узлы сетки, лежащие на средней линии
(см. рисунок снизу для 
).
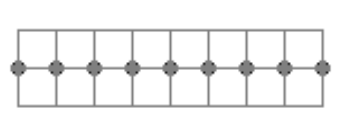
В каждом прямоугольнике таких точек 
. Очевидно, любой Машин отрезок задействует не менее одной отмеченной точки. Значит,
Маша в каждом таком прямоугольнике сможет провести не более 
отрезков. Таким образом, во всём квадрате 
она проведёт не
более 
отрезков. Тогда количество пустых клеток не меньше 
.
Пример. На рисунке снизу показан пример для 
(при других чётных 
примеры аналогичны).
Посчитаем количество пустых клеток
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
