Тема ФЕТТ (Формула Единства / Третье Тысячелетие)

Комбинаторика и комбигео на ФЕ

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела фетт (формула единства / третье тысячелетие)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#85910

Лес представляет собой координатную плоскость, в некоторых узлах которой растут ёлки. Всего ёлок больше миллиона. Докажите, что можно срубить более 100000 ёлок так, чтобы расстояние между любыми двумя срубленными ёлками было больше 3. (Узлом называется точка, обе координаты которой целые; ёлки считаем точками.)

Источники: ФЕ - 2024, 11.2 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Когда нас просят доказать, что что-либо возможно, то один из вариантов решения это просто привести пример. Так и в этой задаче, нам нужно придумать пример вырубки ёлок, удовлетворяющей условию.

Подсказка 2

Получается, нам нужно выбрать больше 100000 ёлок так, чтобы расстояние между любыми двумя из них было больше 3. Может быть не понятно, по какому принципу их вообще выбирать. В таких случаях полезно каким-либо образом разбить ёлки на группы так, чтобы одна из групп была искомой. Но на какое количество групп разбивать?

Подсказка 3

Вспомним принцип Дирихле и посмотрим на числа. Заметим, что если разбить ёлки на 10 групп, то в одной из них точно будет больше 100000 штук. Тогда нам нужно, чтобы внутри каждой группы расстояния между любыми двумя ёлками было более 3.

Подсказка 4

Если не получается придумать разбиение, попробуйте посмотреть на эту задачу по-другому. Например, попытаться разбивать не ёлки, а узлы. Так же не забывайте про количество групп, попробуйте использовать остатки при делении на 10.

Показать доказательство

Раскрасим узлы в 10 цветов так, чтобы узлы одного цвета образовывали сетку из квадратов со стороной $√10$ . Например, пусть цвет узла с координатами ( $x,y$ ) определяется остатком от деления числа $x+ 3y$ на 10 (считаем, что деревья растут в центрах квадратов):


0	1	2	3	4	5	6	7	8	9	0

7	8	9	0	1	2	3	4	5	6	7

4	5	6	7	8	9	0	1	2	3	4

1	2	3	4	5	6	7	8	9	0	1

8	9	0	1	2	3	4	5	6	7	8

5	6	7	8	9	0	1	2	3	4	5

2	3	4	5	6	7	8	9	0	1	2

9	0	1	2	3	4	5	6	7	8	9

6	7	8	9	0	1	2	3	4	5	6
3	4	5	6	7	8	9	0	1	2	3

0	1	2	3	4	5	6	7	8	9	0

По принципу Дирихле, в какой-то из десяти цветов окрасились более 100 тысяч ёлок. Тогда все эти ёлки можно срубить, поскольку расстояние между любыми двумя из них не меньше $√10$ .

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#85912

У Вити есть 9 альбомов с марками, причём в любых двух альбомах количество марок различается. Витя хочет отдать сестре один или два пустых альбома на её выбор. При этом Витя обнаружил, что, какой бы один или какие бы два альбома ни попросила сестра, марки из них можно распределить по остальным альбомам так, что во всех оставшихся семи или восьми альбомах станет поровну марок. Изначально у Вити меньше всего марок в красном альбоме. А какое минимальное количество марок может быть в синем альбоме?

Источники: ФЕ - 2024, 11.4 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Подумаем, а как использовать условие на то, что можно разложить любой альбом по всем остальным альбомам так, чтобы марок в них было поровну? Какой альбом хочется попробовать расформировать?

Показать ответ и решение

Посмотрим, какое минимальное количество марок может изначально быть у Вити в красном альбоме.

_________________________________________________________________________________________________________________________________________________________________________________

Оценка: Упорядочим альбомы по количеству марок, начиная с наименьшего. Если во втором по количеству альбоме $x$ марок, то в следующих не менее чем $x+ 1,x+$ $2,...,x+ 7$ . После расформирования первого альбома в каждом из остальных будет не менее $x+7$ марок, то есть в них надо добавить не менее чем $7+ 6+ ...+ 2+1 +0 =28$ марок.

Пример: 28, 35, 36, ..., 42. Суммарное количество марок тут делится на 7 и на 8 ( $336=$ $42⋅8= 48⋅7$ ), поэтому можно сделать как 8 альбомов по 42 марки, так и 7 по 48 марок.

_________________________________________________________________________________________________________________________________________________________________________________

Итак, тогда общее число марок не меньше $28 +29+ ...+ 36$ , к тому же кратно 7 и 8 , а потому не меньше $336= 28+35+ 36+ ...+ 42$ . Если в этой сумме заменить $28+35$ на $31+32$ , то получим пример к ответу 32.

Предположим теперь, что в синем альбоме 31 марка или меньше. Тогда в красном не более 30 марок. В то же время общее количество марок равно $8a$ , где $a≥42$ . После расформирования красного альбома в остальных нужно сделать ровно по $a$ марок. Значит, изначально в каждом альбоме не более $a$ марок. В синий альбом придётся добавить не менее $42− 31= 11$ марок, а в остальные суммарно не менее чем $6+ 5+ 4+3 +2+ 1+ 0= 21$ марку. Однако в сумме это не менее 32 марок, а в красном альбоме лишь 30.

Ответ: 32

Ошибка.
Попробуйте повторить позже

Задача 3#85913

Вредный учитель даёт ученикам тест из 12 вопросов, на каждый из которых надо ответить «да» или «нет». Учитель не только вредный, но и нечестный, поэтому «правильные» ответы он определяет только после того, как ученики сдадут работы. При этом учитель стремится выбрать «правильные» ответы так, чтобы ни один из учеников не угадал больше половины ответов. При каком наибольшем количестве учеников учитель гарантированно сумеет это сделать?

Источники: ФЕ - 2024, 11.5 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Чтобы учитель смог провернуть свой коварный замысел, нужно чтобы возможных вариантов ответа было больше, чем учеников. Поэтому нам нужно рассмотреть цепочки ответов, но какой длины они должны быть?

Подсказка 2

Нам нужно, чтобы ученики ответили не более, чем на половину вопросов. А для какого числа очень легко посчитать половину? Для двойки! Рассмотрите цепочки ответов длины 2!

Подсказка 3

Существует 4 варианта ответить на два вопроса. Тогда сколько должно быть школьников, чтобы учитель смог сделать один из вариантов правильным? Дорешайте задачу и не забудьте про пример!

Показать ответ и решение

Если учеников три (или меньше), то учитель справится. Действительно, на первые два вопроса возможны 4 варианта ответа: ++, +-, –, -+. Поскольку учеников не больше трёх, то какую-то из этих комбинаций никто не выбрал, её-то учитель и объявляет «правильной». Так же он поступает с каждой следующей парой ответов. В результате у каждого ребёнка не больше половины верных ответов.

Четыре ученика смогут «обыграть» учителя. Для этого им надо разделить вопросы на две группы нечётного размера (например, первые 5 и последние 7 вопросов) и дать такие ответы: ++++++++++++,————, +++++——-,—–+++++++. Тогда найдётся ребёнок, угадавший больше половины ответов как в первой группе, так и во второй.

Ответ: 4

Ошибка.
Попробуйте повторить позже

Задача 4#74787

Маша нарисовала на клетчатой бумаге по линиям сетки квадрат $n ×n$ клеток, где $n−$ чётное число. В некоторых клетках она провела диагонали, соблюдая два правила: - нельзя проводить две диагонали в одной клетке; - нельзя проводить две диагонали с общим концом.

Какое наименьшее число пустых клеток могло остаться на Машином рисунке?

Источники: ФЕ-2022, 11.4 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Очень часто в задачах на оценку и пример бывает полезно разбить доску на фигуры, в которых удобнее делать оценку. Заметим, что в каждом узле не может «встретиться» более одной диагонали.

Показать ответ и решение

Оценка. Разобьём квадрат $n× n$ на $n∕2$ горизонтальных прямоугольников $2×n$ . Докажем, что в каждом из них Маша может провести не более $n+ 1$ отрезка, соблюдая условие задачи. Для каждого такого прямоугольника отметим все узлы сетки, лежащие на средней линии (см. рисунок снизу для $n= 8$ ).

$PIC$

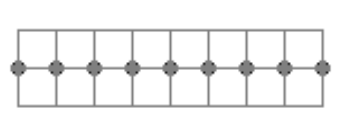
В каждом прямоугольнике таких точек $n+ 1$ . Очевидно, любой Машин отрезок задействует не менее одной отмеченной точки. Значит, Маша в каждом таком прямоугольнике сможет провести не более $n+ 1$ отрезков. Таким образом, во всём квадрате $n ×n$ она проведёт не более $(n +1)⋅n∕2$ отрезков. Тогда количество пустых клеток не меньше $n2− n(n+21)= n(n2−1)$ .