18.05 Алгебра. Связь между множествами решений

Первое решение.

Поймём, что данное следствие реализуется, если множество решений первого неравенства полностью содержится в множестве решений второго. Посмотрим, как выглядят эти множества решений.

Решим второе неравенство

Теперь рассмотрим решение первого неравенства в зависимости от

При Видно, что

Значит, подходят.

При Видно, что

Значит, подходит.

При Посмотрим как должны располагаться множества на числовой прямой

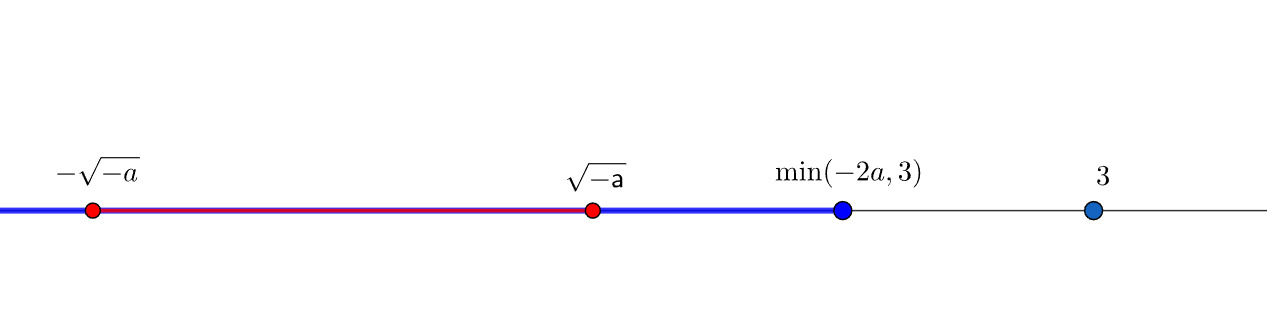
Из этого понимаем, что нужные будут удовлетворять условию

Решаем систему с учётом, что получаем

В итоге, объединив все случаи, получаем _____________________________________________

Второе решение.

Введем плоскость . В ней решением неравенства при конкретном будет пересечение прямой с областью, которая задается неравенством. То, что одно уравнение является следствием другого, означает, что пересечение прямой с множеством, задаваемым вторым неравенством, будет полностью содержать в себе пересечение прямой с множеством, задаваемым первым неравенством.

Неравенство задает область "под параболой" .

Неравенство представим в виде равносильной совокупности:

Эта система на плоскости представляет собой вертикальную прямую и область, лежащую "ниже"прямой и "левее"c

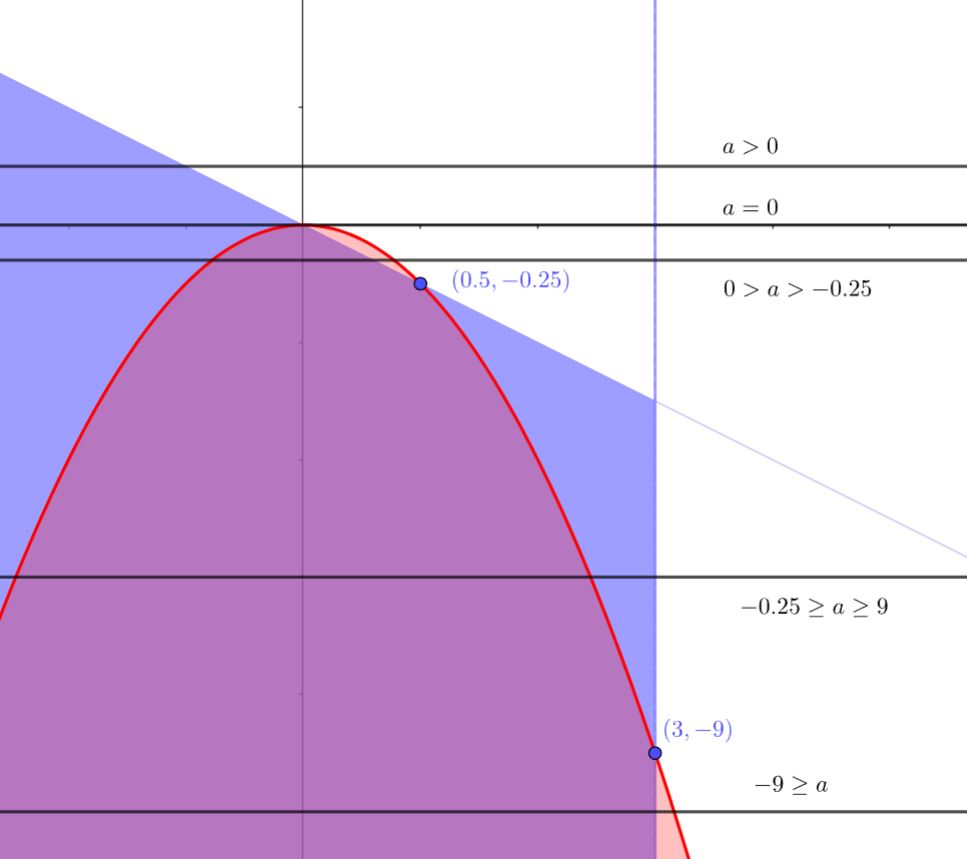
Теперь проанализируем решения неравенств при каждом .

1 случай.) .

При таких значениях первое неравенство не имеет решений. Значит, любое другое неравенство будет его следствием.

2 случай.) .

Решением первого неравенство будет , а решением второго . Т.е. второе неравенство является следствием первого.

3 случай.) .

Как мы видим из рисунка, существуют точки "внутри"параболы, которые не принадлежат области второго неравенства. Т.е. второе неравенство не будет следствием первого.

4 случай.) .

При таких значениях все решения первого неравенство лежат внутри множества решений второго. Т.е. второе неравенство —- следствие первого.

5 случай.) .

При таких значеиях среди решений первого неравенства есть решения . Но у второго неравенства таких решений быть не может. Т.е. второе неравенство не является следствием первого.

Итого получаем