14.08 Тела вращения. Доказательство базовых фактов

Пусть полуплоскости и — грани двугранного угла. Отметим произвольную точку на ребре двугранного угла и проведем через нее плоскость . Тогда , . Получили линейный угол данного двугранного угла. Пусть — его биссектриса. Тогда все точки этой биссектрисы равноудалены от сторон угла . Отметим на биссектрисе точку такую, чтобы , где , . Тогда — центр искомого шара и , — его радиусы (отрезки, перпендикулярные плоскостями и ).

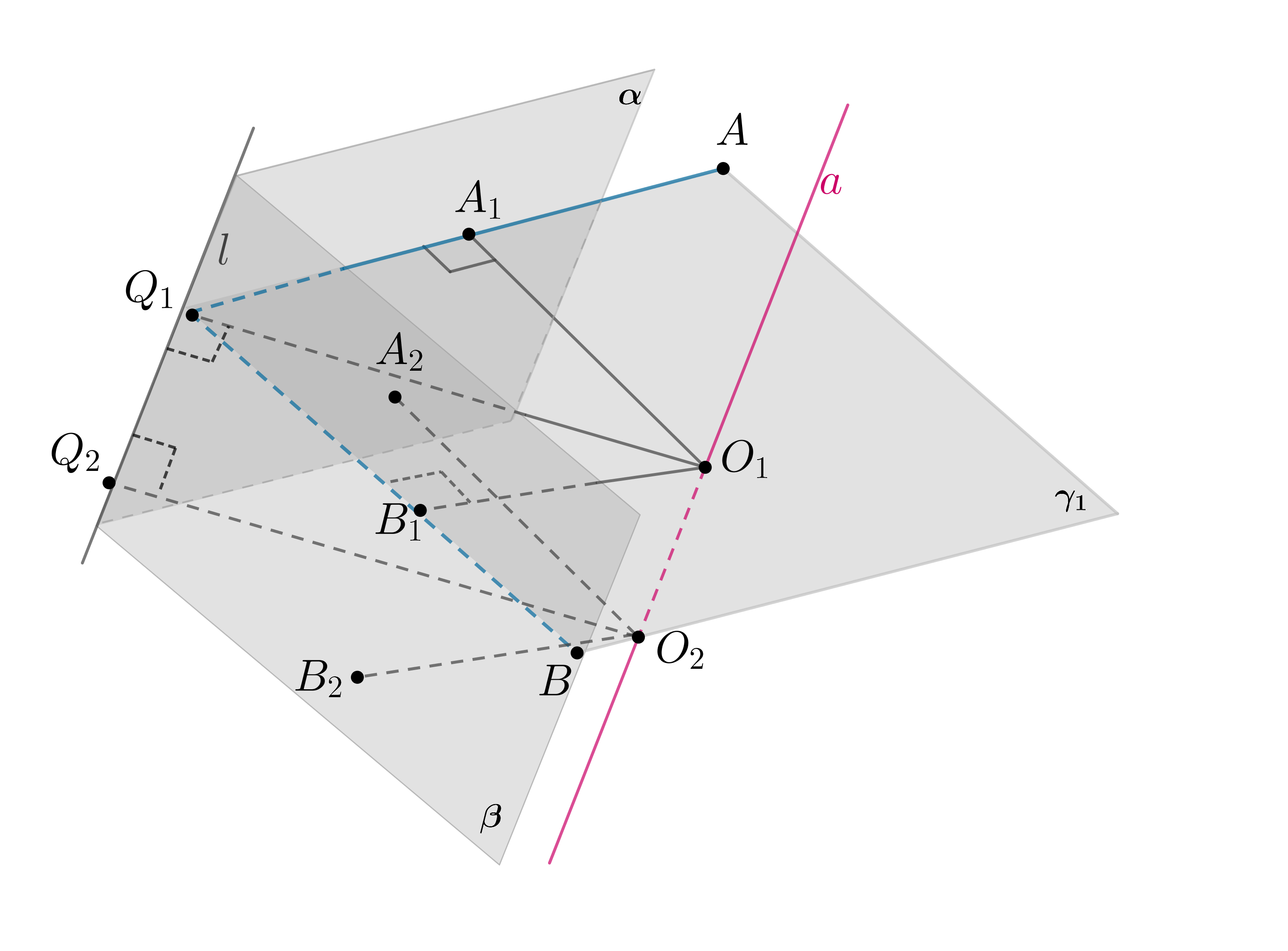
Аналогично построим , , , — линейный угол данного двугранного угла, — биссектриса этого линейного угла.

Тогда как пряомугольные по катету и острому углу . Следовательно, .

Тогда — прямоугольник, так как , и . Следовательно, .

Тогда геометрическое место точек, являющихся центрами шаров радиуса , равноудаленных от и — это прямая , параллельная ребру двугранного угла, удаленная от граней и двугранного угла на расстояние