14.16 Угол между плоскостями
Ошибка.
Попробуйте повторить позже
В цилиндре параллельно диаметру в нижнем основании проведена прямая, пересекающая окружность нижнего основания
в точках
и
причем
Через отрезок
проведена плоскость
под углом
к плоскости осевого сечения
Найдите расстояние от центра нижнего основания до плоскости
Так как то плоскость
пересечет плоскость
по прямой
параллельной
Если это не так,
то
Это противоречит условию, так как прямые и
параллельны.
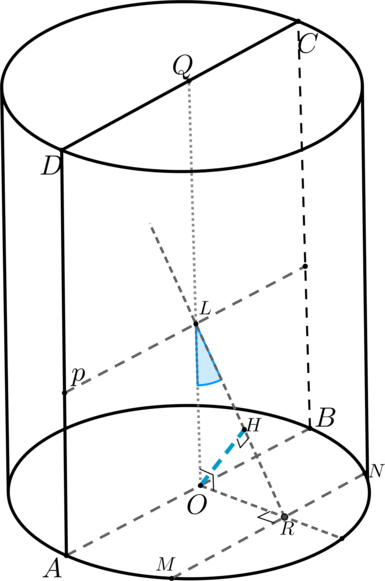
Обозначим за ось цилиндра. Тогда
и
При этом
Проведем Тогда по теореме о трех перпендикулярах
и
Следовательно,
— угол между
плоскостями
и
.
Так как и
то перпендикуляр из точки
на плоскость
упадет на прямую
Рассмотрим В нем имеем:
Рассмотрим прямоугольный В нем имеем:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




