Гармонический четырёхугольник
Ошибка.
Попробуйте повторить позже
Пусть — диаметр окружности
,
— окружность с центром в точке
и радиусом меньше, чем у
. Окружности
и
пересекаются в точках
и
. Хорда
окружности
пересекает вторую окружность
в точке
. Найдите длину отрезка
,
если
.
Источники:
Подсказка 1
Давайте продлим отрезок OB до пересечения с окружностью ω и назовём точку их пересечения N, аналогично продлим DB и назовем их точку пересечения M. Что тогда можно сказать про углы ABC, DBA и MBN?
Подсказка 2
Дуги OC и OD равны в силу симметрии относительно диаметра OP. Значит, ∠ABC = ∠DBA, а ∠DBA и ∠MBN равны, как вертикальные. Что тогда можно сказать про точки M и C, а также отрезки BC и BM?
Подсказка 3
Точки M и C симметричны относительно перпендикуляра к AB, проходящего через точку B, следовательно, отрезки BC и BM будут равными. По условию нам дано CB*BD = 5, следовательно, MB*BD = 5. На какую теорему нам сразу же намекает такое произведение?
Подсказка 4
Когда мы видим произведение отрезков одной хорды, то сразу же нужно вспомнить теорему о пересекающихся хордах, запишем её: MB*BD = AB*BN. Отлично, теперь у нас появилось нужное нам AB, но также появился отрезок BN, про который нам ничего неизвестно. Подумайте, как можно заменить BN?
Подсказка 5
Давайте заметим, что треугольник APN – равнобедренный, а ∠ABP = 90°, в таком случае отрезок PB является высотой и медианой, а BN = AB.
Пусть и
– вторые точки пересечения с окружностью
прямых
и
соответственно. В силу симметрии относительно
прямой
, дуги
и
равны. Следовательно,
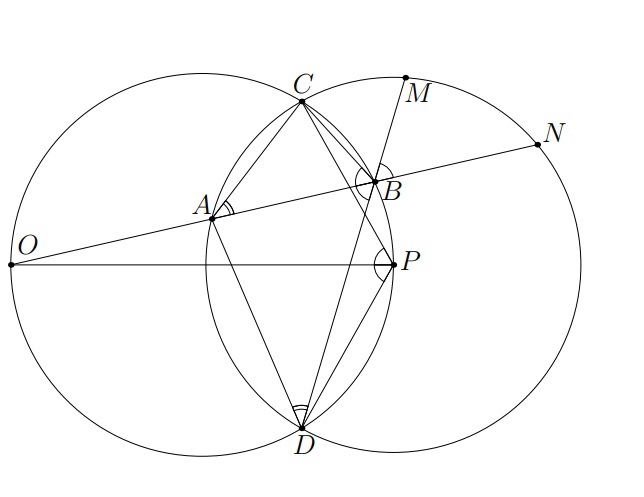
Первое решение.
Обозначим эти равные углы через . Из вписанности четырёхугольника
получаем, что
. Следовательно,
поскольку
– центр
, имеем
C другой стороны,
. Вычитая общую дугу
,
получаем, что
, откуда
Значит, , и треугольники
и
подобны по двум углам, откуда
, так что
______________________________________________________________________________________________________________________________________________________
Второе решение.
Заметим, что , как вписанный угол в окружности
, опирающийся на её диаметр
, поэтому
является высотой и
биссектрисой треугольника
. Получаем, что точки
и
симметричны относительно прямой
, так что
В
окружности
по теореме о пересекающихся хордах
Тогда
откуда сразу получаем
ответ.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание.
В ходе первого решения мы выяснили, что . То есть прямые
и
симметричны относительно
биссектрисы угла
. А во втором решении замечено, что
— середина стороны
Тогда оказывается, что точка лежит на симедиане треугольника
. А сама задача тесно связана со следующим фактом:
окружность, проходящая через концы одной диагонали гармонического четырёхугольника и центр описанной около него
окружности, делит другую его диагональ пополам. Вы могли встретить его в такой задаче: пусть
— центр описанной
около треугольника
окружности,
— середина стороны
описанные около треугольников
и
окружности вторично пересекаются в точке
Тогда прямые
и
симметричны относительно биссектрисы угла
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




