Гармонический четырёхугольник
Ошибка.
Попробуйте повторить позже
Четырехугольник вписан в окружность
с центром
Биссектриса угла
пересекает отрезок
в точке
и
окружность
второй раз в точке
Биссектриса угла
пересекает отрезок
в точке
и окружность
второй раз в точке
Известно, что прямые
и
параллельны. Докажите, что описанная окружность треугольника
проходит через середину
отрезка
Подсказка 1
Мало у каких четырехугольников середина диагонали - хорошая точка. А у каких хорошая? У гармонических. Поймете, где на чертеже должен быть гармонический четырехугольник.
Подсказка 2
Оказывается, BDMN должен быть гармоническим. Как это сделать? Какие точки полезно отмечать у гармонических четырехугольников?
Подсказка 3
В условии есть параллельность, она дает какие-то отношения, биссектрисы тоже дружат с отношениями. Из них получите, что BDNM - гармонический. Отметьте точку пересечения касательных в точках M и N. После этого поймите, что все 5 точек M, O, N, середина BD и точка пересечения касательных, лежат на одной окружности.
Гомотетия с центром в точке переводит точки
в точки
соответственно, поскольку
Прямые
и
при ней же перейдут в касательные в точках
и
к окружности
поскольку последние параллельны
прямым
и
Наконец, точка
перейдет в точку пересечения
указанных касательных, а значит, лежит на
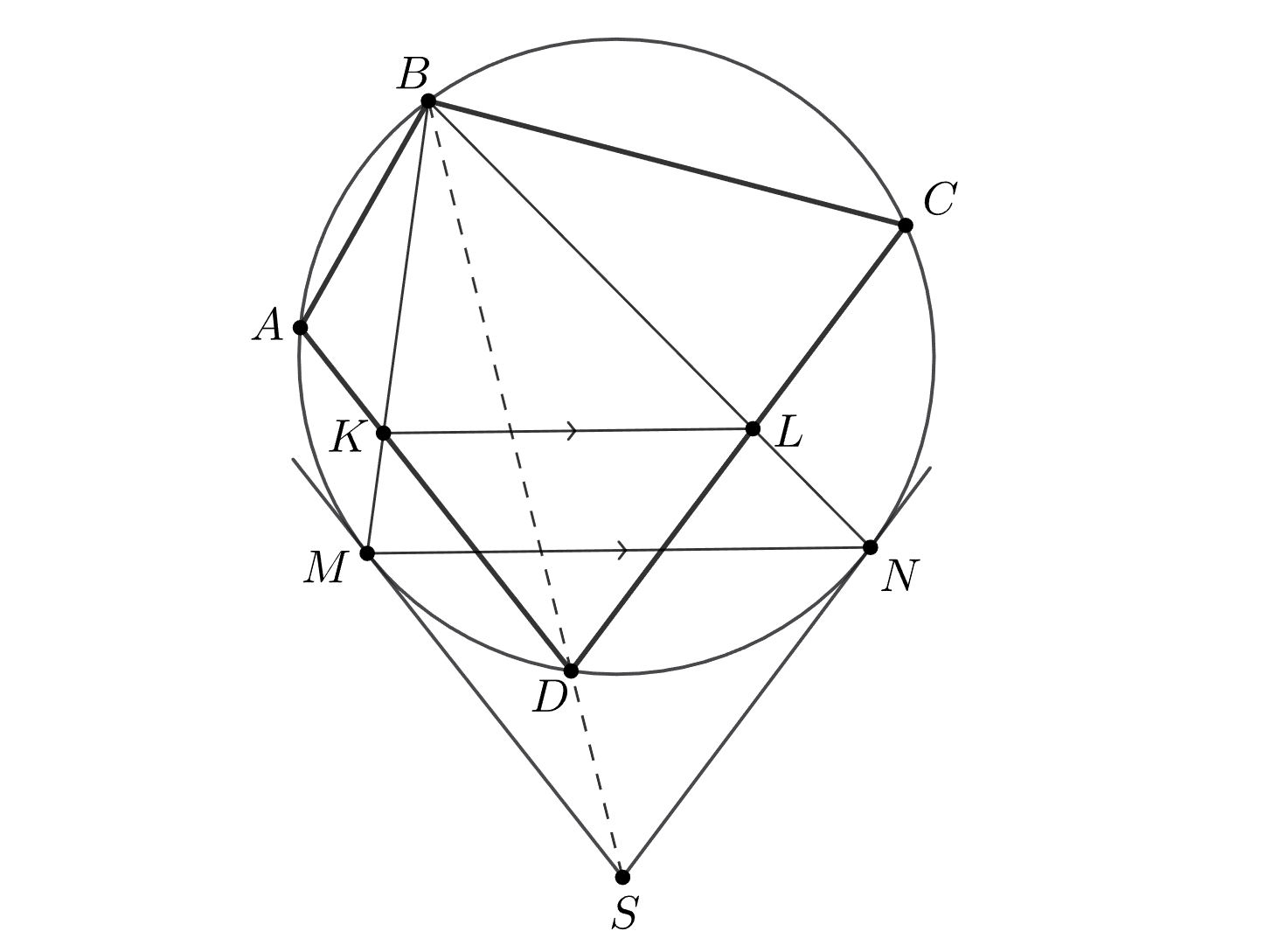
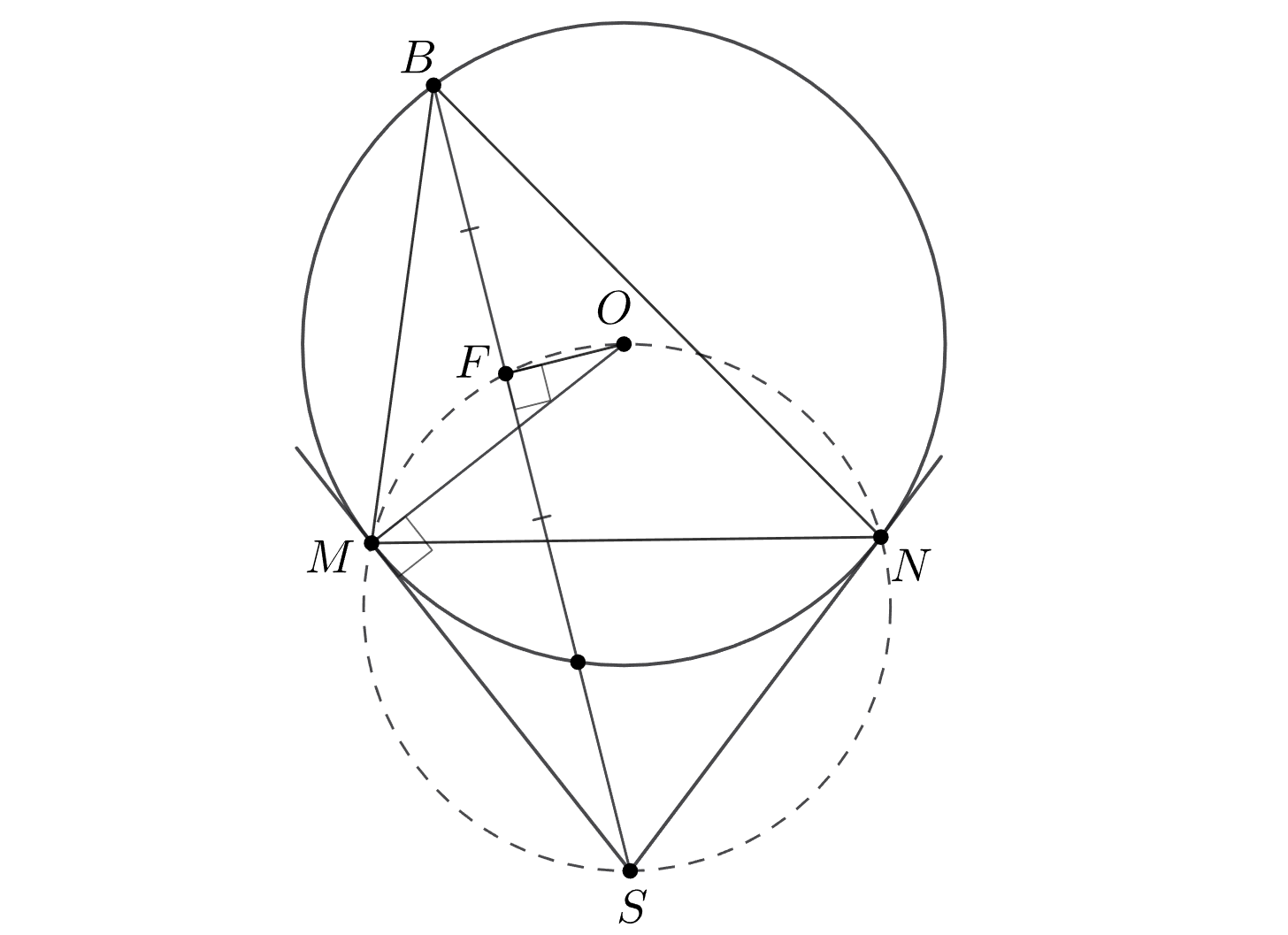
Осталось заметить, что углы
прямые, то есть точки
лежат на окружности с диаметром
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




