Среднее арифметическое в текстовых задачах

Мы всегда считаем, что площадь торта равна

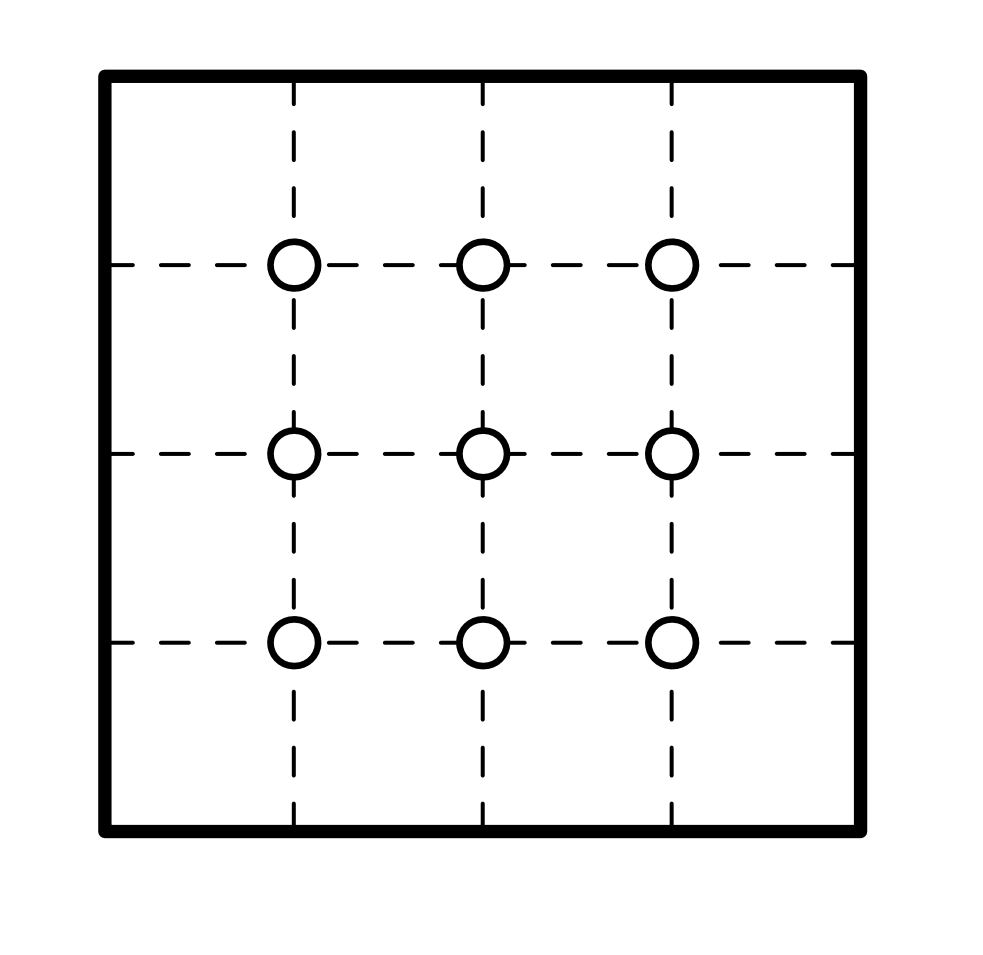
Покажем, что при некоторых запросах детей родители не смогут вырезать более требуемых кусков. Выберем число Предположим, что главных детей заказали по куску торта площади (а остальные трое сделали произвольные заказы так, чтобы суммарная площадь заказанных кусков была равна 1). Мысленно разобьём торт на 16 равных квадратов и отметим на торте все 9 вершин этих квадратов, не лежащих на границе торта (см. рисунок ниже). Тогда строго внутри любого квадратного куска площади будет лежать одна из отмеченных точек, то есть можно вырезать не больше девяти таких кусков. Значит, хотя бы шестерым детям желаемых кусков не достанется.

Осталось доказать, что детей всегда смогут получить желаемое. Пусть

— длины сторон кусков, которые хотят получить дети, то есть

Покажем, что из квадрата можно вырезать куски со сторонами

Для этого нам потребуются неравенства

Для доказательства первого неравенства заметим, что

в последнем переходе мы воспользовались неравенством между средним квадратичным и средним арифметическим. Второе неравенство доказывается аналогично:

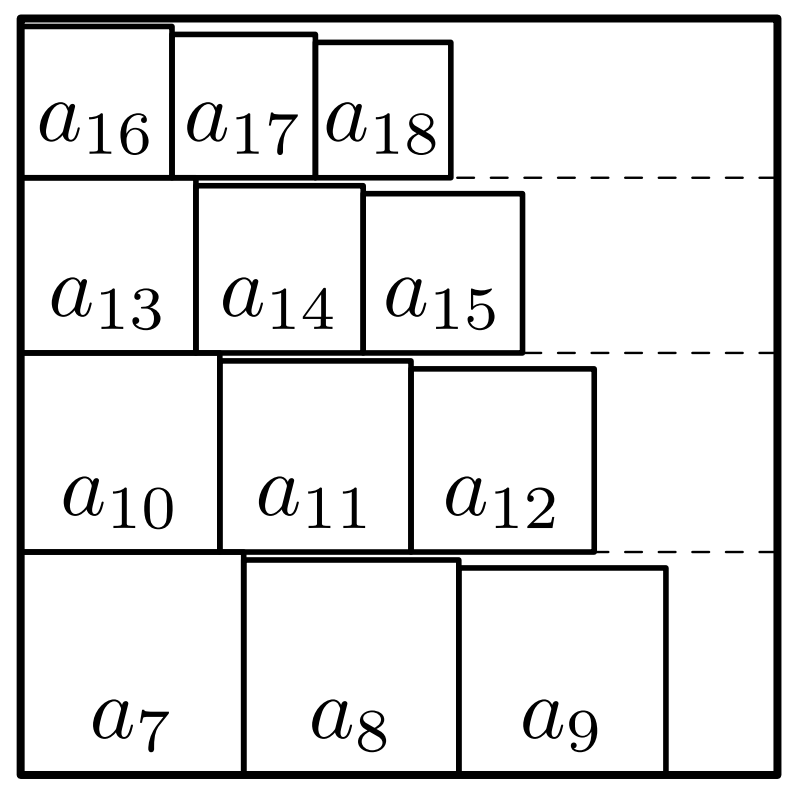
Из неравенств следует, что можно разрезать торт на горизонтальные полосы высот, не меньших и соответственно, и в -ю полосу уложить квадраты со сторонами и как показано на рисунке ниже.