Подсчеты в клетчатых задачах
Ошибка.
Попробуйте повторить позже
Клетки доски покрашены в черный и белый цвет. Известно, что для каждой черной клетки в «кресте» из строчки и столбца, на
пересечении которых она находится, не менее
белых клеток. Какое наибольшее количество клеток доски могут быть
черными?
Подсказка 1
Давайте придумаем некоторый пример. Интуитивно мы хотим, чтобы в нем для каждой черной клетки количество белых, находящихся в ее кресте, было как можно более приближено к 2k. Можно ли придумать пример, когда для всех черных клеток это число равно 2k?
Подсказка 2
Да, пусть в первой строчке белыми будут клетки 1, 2, …, k, во второй — 2, 3, …, k+1 (то есть на каждой следующей строчке сдвигаем все на 1 вправо, возможно, с переносом в начало). Сколько черных клеток получается при такой раскраске?
Подсказка 3
В каждой строке количество белых клеток равно k, а значит, во всей доске kn, следовательно, количество черных клеток при такой раскраске равно n²-nk. Давайте докажем, что это наибольшее число клеток.
Подсказка 4
Мы хотим получить оценку на количество черных клеток. При этом достаточно показать, что количество белых клеток всегда по крайней мере nk. Предположим, что в строчках стоят a_1, a_2, …, a_n белых клеток, а в столбцах — b_1, b_2, ...., b_n белых клеток. Заметим, что в i-строке пересечении с n-a_i столбцами у неё стоят черные клетки. Значит, в каждом из этих столбцов не менее 2k-a_i белых клеток. Просуммируем такие величины по всем строкам. Дайте оценку сверху на количество посчитанных раз фиксированной белой клетке из j-столбца.
Подсказка 5
Заметим, что белую клетку из j-ого столбца мы посчитали не более n-b_j раз. То есть имеем неравенство (n-a_1)(2k-a_1)+(n-a_2)(2k-a_2)+...+(n-a_n)(2k-a_n) ≤ b_1(n-b_1)+b_2(n-b_2)+...+b_n(n-b_n). Наша цель --- отойти от использования переменных a_1, …, a_n, b_1, …, b_n и перейти к количеству белых клеток s=a_1+a_2+...+a_n. Для этого преобразуйте исходное неравенство.
Подсказка 6
После преобразований мы получим 2n^2k-2(n+k)(a_1+a_2+...+a_n)+a_1^2+a_2^2+...+a_n^2+b_1^2+b_2^2+....+b_n^2 ≤ 0. Как мы можем оценить снизу сумму квадратов через сумму переменных? Это нужно, чтобы окончательно перейти к неравенству, в котором будут фигурировать только переменный n, k и s.
Подсказка 7
По неравенству между средним квадратичным и арифметическим, мы имеем a_1^2+a_2^2+...+a_n^2 <= (a_1+a_2+...+a_n)^2/n. То есть мы можем переписать неравенство в виде 2n^2k-2(n+k)(a_1+a_2+...+a_n)+ (a_1+a_2+...+a_n)^2/n+ (b_1+b_2+...+b_n)^2/n = 2(s^2/n - (n+k)s+n^2k) ≤ 0. Теперь у нас есть все, чтобы получить оценку на количество s белых клеток.
Подсказка 8
Для этого достаточно показать, что s^2/n ≥ sk - nk^2. Докажите данное неравенство и поставьте его в полученную на предыдущем шаге оценку.
Оценка. Предположим, что в строчках стоят белых клеток, а в столбцах —
белых клеток. Рассмотрим
-ую
строку. Заметим, что в пересечении с
столбцами у неё стоят черные клетки. Значит, в каждом из этих столбцов не менее
белых клеток. Просуммируем такие величины по всем строкам. Заметим, что белую клетку из
-ого столбца мы посчитали не более
раз. То есть имеем неравенство
Раскрыв скобки и перенеся все в левую сторону, а также воспользовавшись тем, что
имеем
По неравенству между средним квадратическим и арифметическим, имеем
Тогда
Обозначим количество белых клеток через
Тогда после сокращения на получаем
С другой стороны, по неравенству между средним арифметическим и геометрическим, имеем
То есть
откуда получаем
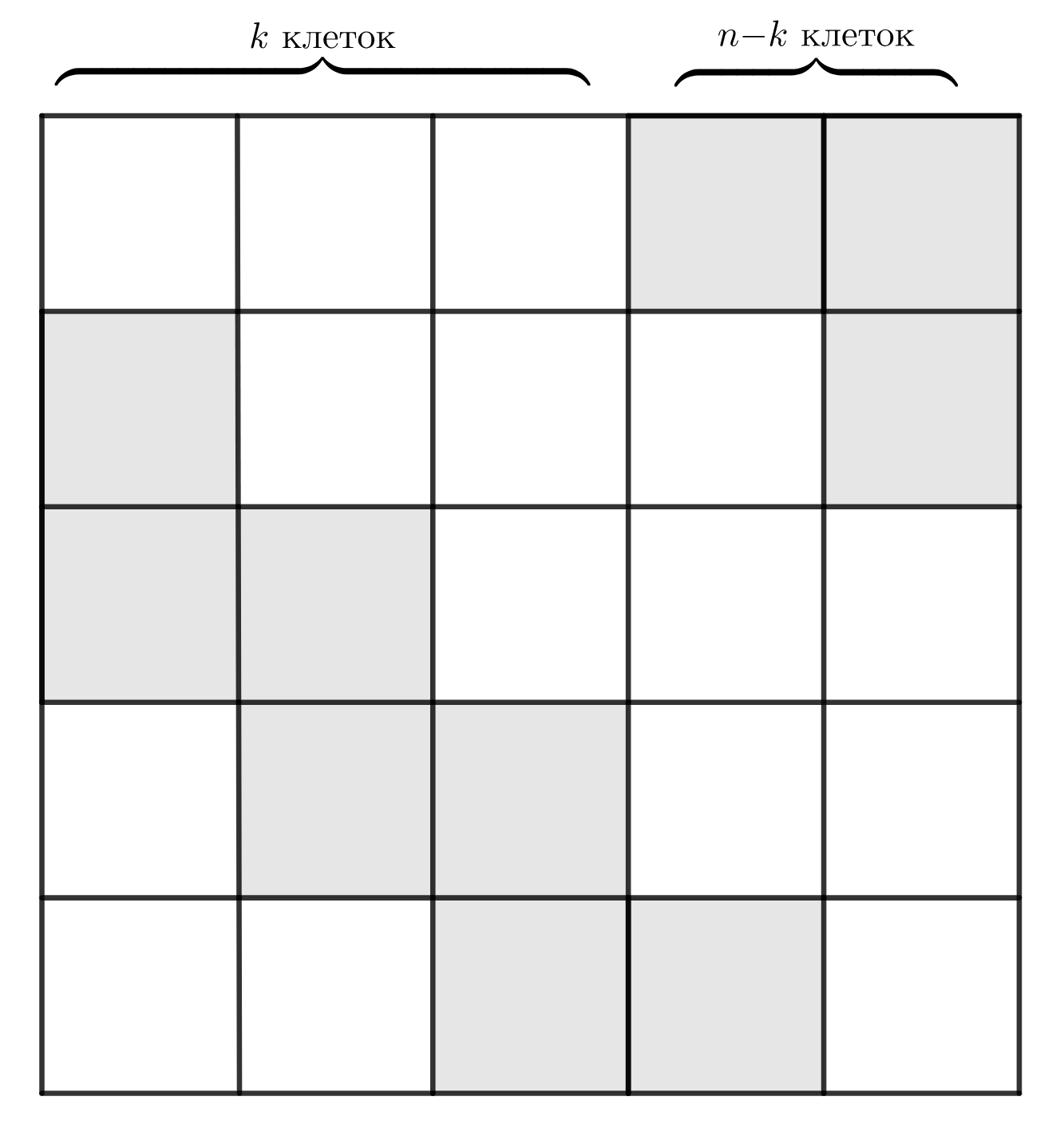
Пример. Пусть в первой строчке белыми будут клетки во второй —
…(то есть на каждой следующей
строчке сдвигаем все на
вправо, возможно, с переносом в начало). Таким образом, в каждой строчке и в каждом столбце
будет ровно
белых клеток. Оставшиеся клетки будут черными, в кресте каждой из них будет ровно
пустых
клеток.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




