Подсчеты в клетчатых задачах

Лемма. В любой гармонической расстановке либо в каждой строке, либо в каждом столбце находится ровно буквы.

Доказательство. Заметим, что если существует строка, в которой подряд идут три различные буквы то в каждом столбце встречаются ровно буквы. Действительно, под мы можем поставить лишь букву четвертую в соседней от нее клетке слева стоит буква справа — Таким образом мы можем заполнить все рассматриваемые столбцы, в которых стояли различные буквы.

Первый столбец справа от уже рассмотренных стоят, чередуясь, буквы и в каком-то порядке. Аналогичными рассуждениями получим, что в любом столбце чередуются две буквы.

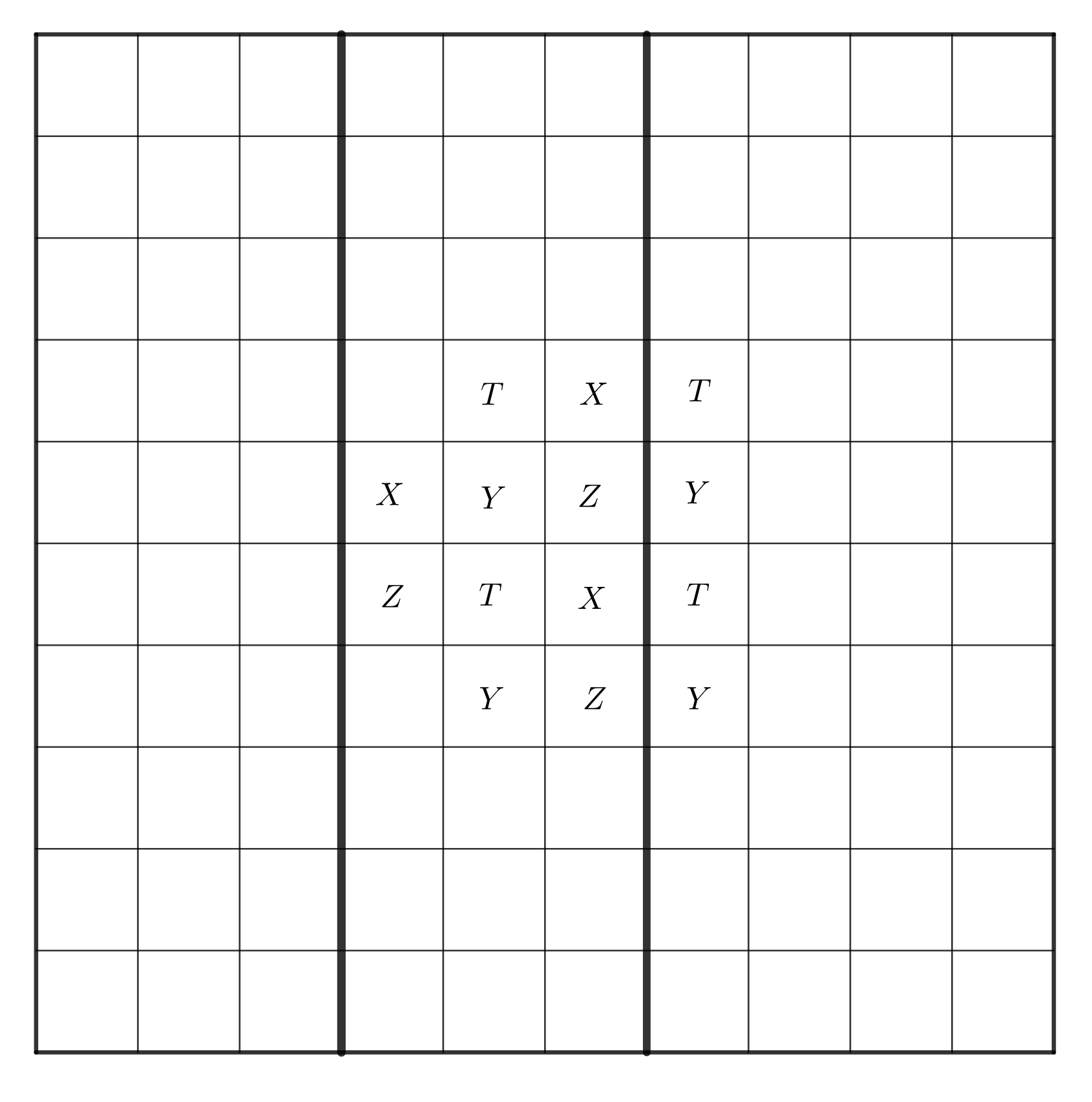
Аналогично, если существует столбец, в котором подряд идут три различные буквы, то в каждой строке чередуются две буквы. Если на доске такой строки и столбца не существует, то в каждой строке и в каждом столбце чередуются ровно буквы.

_________________________________________________________________________________________________________________________________________________________________________________

Таким образом, количество гармонических раскрасок равно сумме количеств гармонических расстановок, в которых два числа чередуются во всех столбцах или во всех строках, без количества гармонических расстановок, в которых два числа чередуются и там, и там.

Найдем количество гармонических расстановок, в которых в каждом столбце находятся ровно две буквы. Существует способа заполнить верхний левый квадрат, который однозначно определяет буквы во всех клетках двух самых левых столбцов. Соседний к ним слева столбец можно заполнить двумя способами, как и каждый последующий. Таким образом, число равно Этому же числу равно число расстановок, в которых в каждой строке находятся ровно две буквы.

Каждая расстановка, в которой две буквы чередуются и во всех строках, и во всех столбцах, однозначно определятся заполнением первого квадрата, а значит, их количество равно Наконец, количество гармонических расстановок, равно