Подсчеты в клетчатых задачах
Ошибка.
Попробуйте повторить позже
В каждой клетке квадрата записано вещественное число от
до
Рассмотрим всевозможные разрезы этого квадрата на два
прямоугольника по вертикальной или горизонтальной линии сетки. Оказалось, что какой бы разрез не был произведен, сумма чисел хотя бы
в одном из двух получившихся прямоугольников не больше
Найдите максимально возможную сумму чисел в исходном
квадрате.
Подсказка 1
Попробуйте придумать какой-нибудь пример на небольшую сумму и отталкивайтесь от него.
Подсказка 2
Для построения примера можете заполнить по условию какой-то маленький квадрат, а остальные клетки заполнить нулями.
Подсказка 3
Примера надо придумывать на 5. Для оценки попробуйте доказать, что найдётся такое a что если разрезать квадрат по столбцам a и a + 1, то в обоих сумма будет не больше 1. Подумайте, как это поможет оценке.
Если мы расставим и
так, как показано на картинке ниже (в клетках, которых нет на картинке, стоят нули), то мы получим пример
на
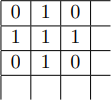
Теперь покажем, что сумма чисел во всех клетках не может быть больше Пусть
Для пары положительных целых чисел
и
определим
как сумму чисел во всех клетках, находящихся в строке с номером, не меньшем
и не большем
(если
то
будем считать, что
).
Пусть — максимальное целое число такое, что
и
Теперь выберем наименьшее целое число
такое, что
и
Выбрать такие
и
можно, поскольку
и
Если
то
а значит из
максимальности
мы имеем
в то время как из минимальности
мы имеем
Таким образом, если
разделить доску по
-ой и
-ой строкам, мы получим два прямоугольника, не удовлетворяющих условию. Следовательно,
Аналогично, если мы определим как сумму чисел в клетках, находящихся в столбце с номером не меньшим
и строкой не
большей
(если
то
), то мы найдём такое число
что
Пусть — число в клетке с на пересечении строки
и столбца
Поскольку
мы можем оценить сумму чисел во всех клетках
как
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




