Разбиение доски на части
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
В клетки таблицы 
вписаны числа 
и 
так, что в клетках каждого квадрата 
стоит ровно три одинаковых числа.
Какое максимальное значение может принимать сумма всех чисел в этой таблице?
Подсказка 1
Каким комбинаторным объектом можно описать сумму чисел в таблице?
Подсказка 2
Количеством единиц в таблице. Таким образом, необходимо минимальное возможное количество нулей в таблице. Как можно оценить количество последних снизу?
Подсказка 3
В каждом квадрате 2 на 2 количество нулей не меньше 1. Какое максимальное количество попарно непересекающихся квадратов можно расположить в таблице?
Подсказка 4
Квадрат целой части от n/2. Осталось придумать пример таблицы, где в каждом квадрате 2 на 2 будет ровно 1 ноль.
Очевидно, что если 
— минимально возможное число нулей в таблице, то искомая сумма достигает максимума, равного числу
В любой таблице 
можно выделить ![[n ]2
2](/api/latex-service/v1/GetSession/219527/index-468d4ef48a495d05a6d3be196aac536e.svg)
непересекающихся 
квадратов, где через ![[n]
2](/api/latex-service/v1/GetSession/219527/index-75fe12d7162276573cc5a168280d3863.svg)
обозначена целая часть числа 
![[n] n
( 2 = 2,](/api/latex-service/v1/GetSession/219527/index-b4fa0e33d2bff5021f8b5e749e807758.svg)
если 
четно; ![[n] n−1
2 = 2 ,](/api/latex-service/v1/GetSession/219527/index-2f9c402f83c458aa7cd62a32b39daaf6.svg)
если 
нечетно). В каждом таком 
квадрате содержится либо три нуля, либо один нуль, т.е.
не менее одного нуля. Тогда во всей таблице 
найдется не менее ![[n]2
2](/api/latex-service/v1/GetSession/219527/index-05bf36a1192e8e55067c50effbae0e17.svg)
нулей, а значит, искомое число ![[n ]2
k = 2 .](/api/latex-service/v1/GetSession/219527/index-9734392931abfb4166bb1ea14fe8379e.svg)
Приведем пример
таблицы 
с минимальным числом нулей, равным ![[n ]2
2 .](/api/latex-service/v1/GetSession/219527/index-02dc1c4b444fd095f533e21adc58577b.svg)
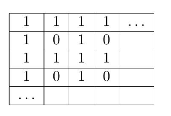
В приведенной таблице нули находятся лишь на пересечении строки и столбца с четными номерами. Таким образом, максимальное
значение суммы всех чисел в таблице равно ![n2− [n2]2.](/api/latex-service/v1/GetSession/219527/index-312ce824af00661ef8f13f8e1c44ae2c.svg)
![n2− [n]2
2](/api/latex-service/v1/GetSession/219531/index-006fa63a2e380bf2f5f39a0008b3dead.svg)
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
