Разбиение доски на части
Ошибка.
Попробуйте повторить позже
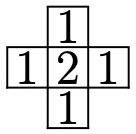
Антон положил на клетчатую доску несколько бумажных крестиков, изображенных на рисунке (каждый крестик покрывает ровно
5 клеток доски). Оказалось, что для каждой клетки доски сумма попавших на неё чисел не превосходит 2. Какое наибольшее количество
крестиков мог положить Антон?
Источники:
Подсказка 1
Понятно, что двойки не могут попасть на рамку. Очень часто в задачах на оценку+пример помогает разбиение на фигуры, в которых мы точно сможем определить количество двоек. На какие?
Подсказка 2
Заметим, что в прямоугольнике 2*3 двоек не больше двух! Осталось лишь придумать пример)
Отметим центральные клетки всех положенных Антоном крестиков. Эти клетки не могут лежать на границе доски, поэтому они
располагаются в прямоугольнике Разобьем его на
прямоугольных блока
Несложно проверить, что в каждом
таком блоке не может находиться больше 2 центральных клеток. Поэтому на доске находится не более
крестиков.
Приведем пример расположения такого количества центральных клеток. Разобьем весь прямоугольник на диагональные ряды
одного направления и отметим все клетки каждой третьей диагонали. В каждую полоску
попадёт ровно одна отмеченная клетка,
поэтому их будет ровно
штуки. Легко убедиться, что условие при этом будет выполняться.
Итого
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




