Планиметрия на Высшей пробе
Ошибка.
Попробуйте повторить позже
Дана двусторонняя линейка без делений. Этот инструмент позволяет делать две операции:
1) провести прямую через две данные точки;
2) провести прямую, параллельную данной, на расстоянии 1 от нее.
Постройте с ее помощью (и не используя никакие другие инструменты) правильный треугольник.
Источники:
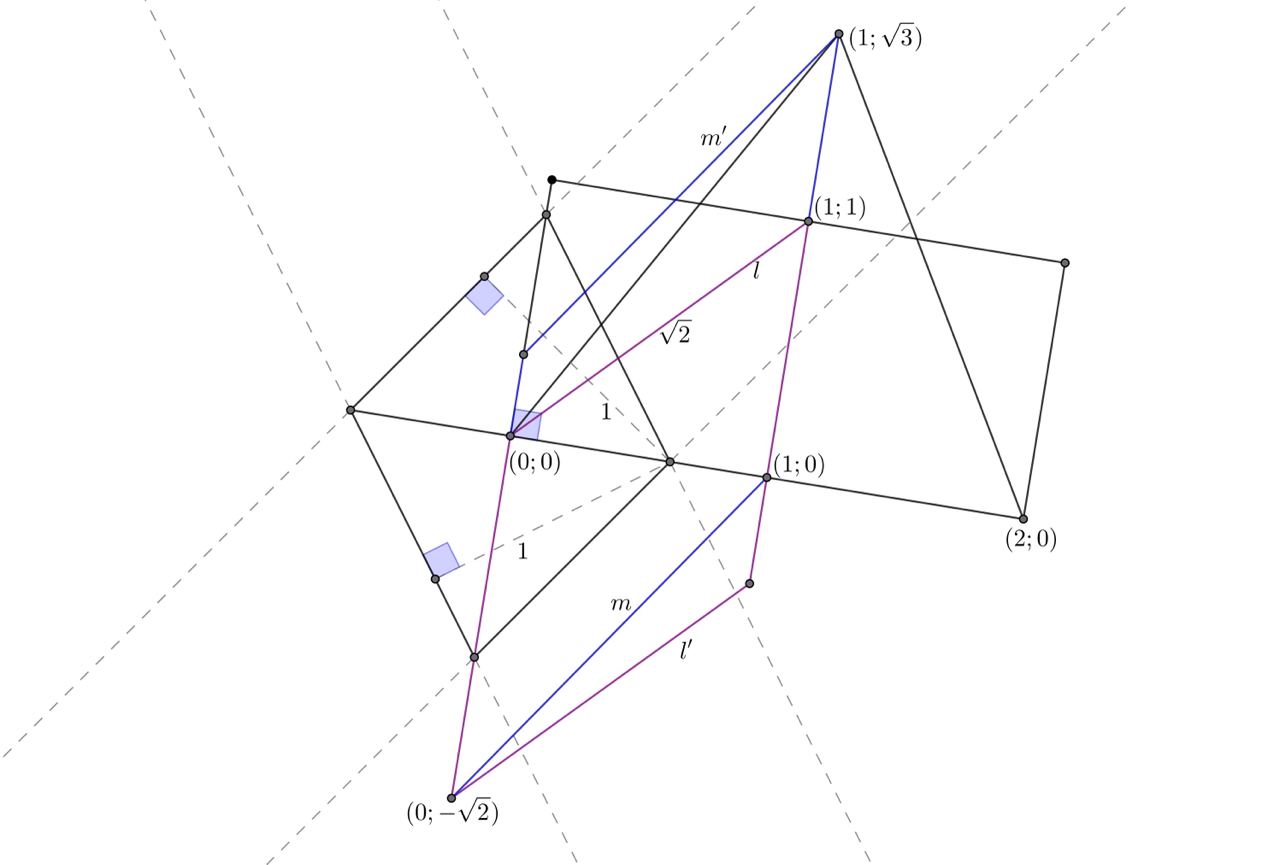
Для начала построим две пары параллельных прямых. На их пересечении образуется параллелограмм с одинаковыми высотами, равными
а значит, являющийся ромбом. Проведем его диагонали, как известно, являющиеся перпендикулярными. Заметим, что с помощью двух
этих перпендикулярных прямых и построения параллельных прямых на расстоянии
мы можем построить клетчатую сетку любого
конечного размера, состоящую из квадратиков со стороной
Введем систему координат с центром в одном из узлов сетки и с осями, параллельными сторонам клеток. Проведем прямую через
точки
и
Теперь проведем снизу от нее параллельную прямую
на расстоянии
Заметим, что на пересечении
пар прямых
и
образуется ромб со стороной длины
а значит,
проходит через точку
Теперь проведем прямую через пару точек
и
а также параллельную ей прямую
на расстоянии
сверху от нее.
На пересечении пар прямых
и
образуется ромб со стороной длины
а значит,
проходит через
точку
Осталось лишь соединить точки и
чтобы получить искомый равносторонний треугольник.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




