Подвешивание, ранжирование, упорядочивание в графах

Пример

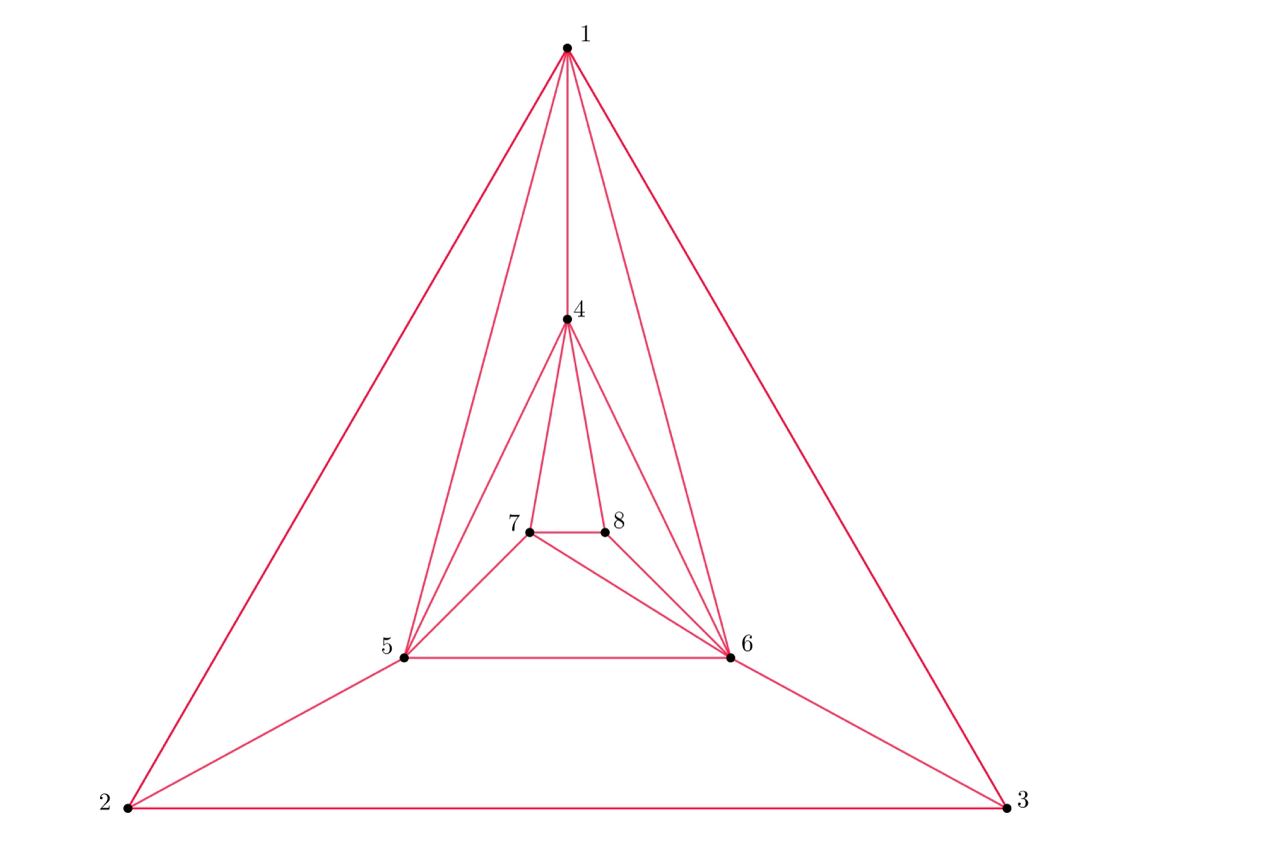
Рассмотрим набор точек, изображенных на иллюстрации. Для простоты восприятия проведем только красные отрезки.

Докажем, что синего треугольника не найдется. Для этого разделим точки на три уровня: точки и будут принадлежать внешнему уровню, точки и — среднему, а и — внутреннему. Заметим, что на каждом уровне все точки соединены между собой красными отрезками, а значит, если синий треугольник существует, все его вершины находятся на разных уровнях.

Вершина соединена со всеми вершинами среднего уровня, а значит, не может быть вершиной синего треугольника. Аналогично, вершина соединена со всеми вершинами внешнего уровня, а значит, не может быть вершиной синего треугольника. Тогда вершина соединена со всеми вершинами среднего уровня, кроме и не может быть вершиной синего треугольника. Значит, ни одна вершина внутреннего уровня не является вершиной треугольника с синими сторонами, а значит, такого треугольника не найдется.

Пример

Возьмем два графа с красными ребрами. Тогда синие отрезки образуют граф в котором, как и любом другом полном двудольном графе, нет треугольников.

Замечание. Если точек или более, то синий треугольник обязательно найдется. Другими словами, граф, дополнительный к планарному на и более вершинах, всегда содержит граф-треугольник в качестве подграфа.