Счёт площадей, рельсы Евклида, теорема о линолеуме
Ошибка.
Попробуйте повторить позже
Дан прямоугольный треугольник Окружность, касающаяся прямой
в точке
пересекает высоту
проведённую к
гипотенузе, в точке
а катет
— в точке
Известно, что
. Найдите отношение площади треугольника
к площади треугольника
Источники:
Подсказка 1
Пупупу… Точки E, F, B – лежат на одной окружности, причем точки E и F соединены! А что нам может помочь найти окружность? Правильно, равные углы. Что надо сделать, чтобы выйти на эти равные углы?
Подсказка 2
Да, нужно соединить все точки, лежащие на этой окружности, то есть надо соединить B с E и B с F! Тогда нетрудно видеть, что ∠CBF=∠FEB(угол между хордой и касательной), а также в силу параллельности ∠FEB=∠ABE! Таким образом, в силу равенства ∠CBF и ∠ABE: при гомотетии с некоторым положительным коэффициентом BF перейдет в BE, поскольку △ABC∼△CDB! Какие соотношения из этого можно написать?
Подсказка 3
Да, поскольку точки E и F разбивают отрезки AC и CD соответственно на два отрезка с одинаковым отношением(это первое соотношение), а также можно применить теорему Фалеса(это второе соотношение)! Какой вывод из этого можно сделать?
Подсказка 4
Верно, получается, что CF=DF! То есть, F – середина отрезка CD. Осталось заметить лишь одно подобие треугольников, какое же?
Подсказка 5
Верно, △ACD∼△ECF, потому что EF – средняя линия △ACD! Теперь нужно только расписать отношение площадей!
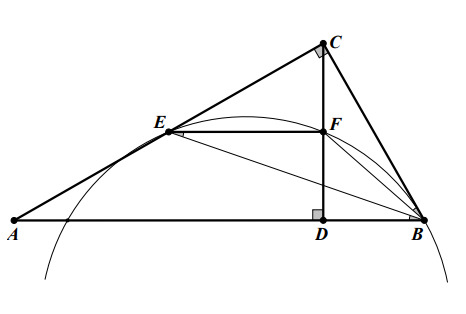
Соединим точку с точками
и
Так как
то
а
по теореме об угле между касательной и хордой. Поэтому
Следовательно,
и
— соответствующие элементы в подобных прямоугольных треугольниках
и
(По
двум углам:
— общий и
Значит,
По обобщённой теореме Фалеса
Из полученных равенств следует, что
Значит, — середина
а так как
то
— средняя линия
Отсюда
А значит,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




