Вписанная сфера
Ошибка.
Попробуйте повторить позже
Дана правильная призма с основанием
Плоскости
и
перпендикулярны
и проходят через вершины
и
соответственно. Пусть
и
соответственно — точки пересечения плоскостей
и
с диагональю
, при этом
(b) Пусть дополнительно известно, что некоторая сфера радиуса 3 касается всех боковых граней призмы, а также плоскостей и
Найдите отрезок
и объём призмы
Пункт а, подсказка 1
Посмотрите на плоскость α. Через какие еще точки она должна пройти?
Пункт а, подсказка 2
Например, она должна пройти через точку С.
Пункт а, подсказка 3
А если рассмотреть B₁H и DF как проекции?
Пункт б, подсказка 1
Как мы можем воспользоваться сферой?
Пункт б, подсказка 2
Рассмотрите ее проекцию на основание ABCD.
Пункт б, подсказка 3
Найдите расстояние между плоскостями α и β.
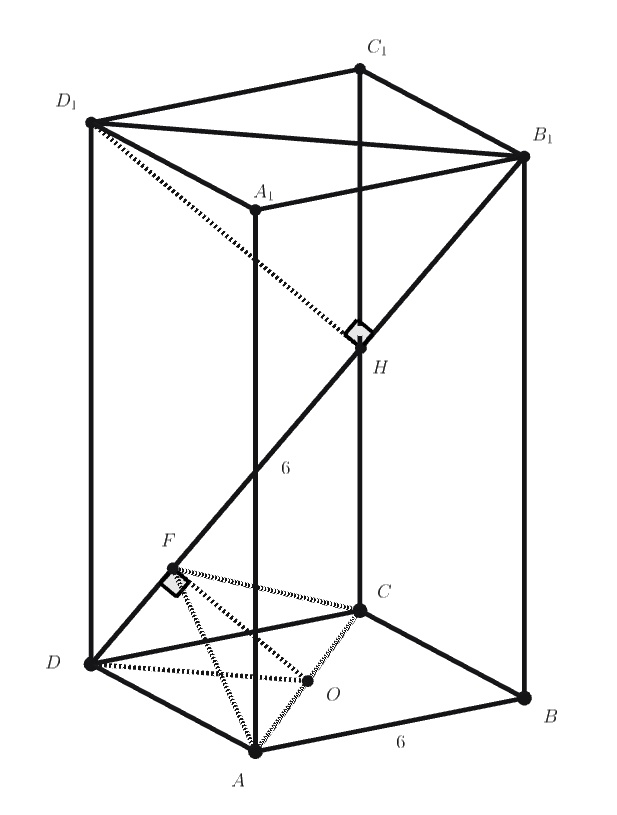
(a) Из соображений симметрии (относительно плоскости плоскость
проходит через точку
— и, значит, через центр
грани
Отрезки
и
— проекции параллельных отрезков
и
на прямую
причём
Значит,
(b) Поскольку сфера касается всех боковых граней призмы, её проекция на основание есть окружность, вписанная в это основание.
Значит, Кроме того,
и
— это две параллельные плоскости, касающиеся сферы, поэтому расстояние
между ними равно диаметру сферы, то есть
Так как
этим расстоянием является отрезок
поэтому
Обозначим Поскольку
— высота прямоугольного треугольника
то
и, следовательно, Тогда
и
Получаем уравнение
поскольку
Наконец, высота призмы равна
А объём призмы равен
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




