Вписанная сфера

Пусть сфера вписана в тетраэдр Будем её раздувать так, чтобы она оставалась вписана в трёхгранный угол при вершине пока она не коснётся одной из граней тетраэдра Без ограничения общности, полученная сфера касается грани Докажем, что она также касается граней и Из этого последует, что — центры гомотетий с положительными коэффициентами, переводящими в и а в В таком случае точки и лежат на одной прямой.

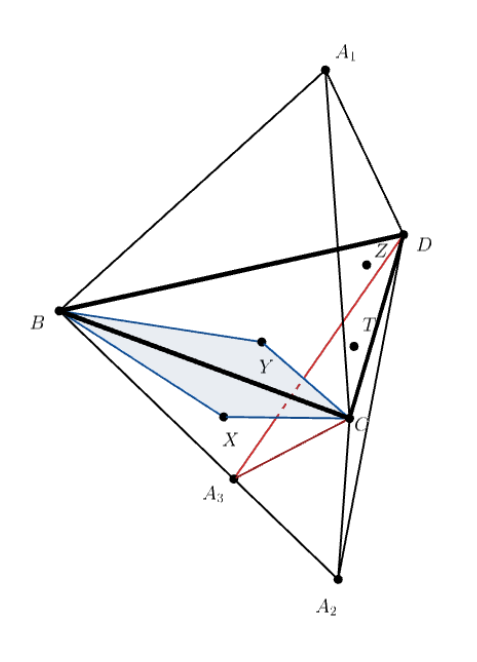
Пусть сфера не касается грани Тогда на ребре найдётся точка такая, что плоскость касается сферы в некоторой точке Обозначим точки касания с плоскостями за соответственно. Тогда имеется четыре пары равных треугольников: и и и и Следовательно,

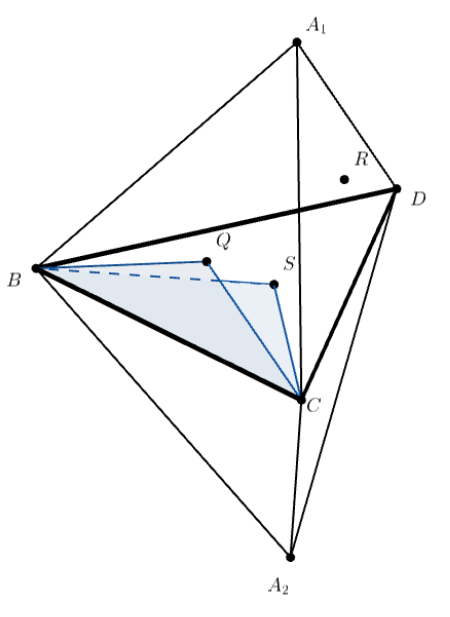
Пусть сфера касается граней в точках соответственно. Тогда треугольники и и и равны. Значит,

Аналогично,

Из равенства крайних членов получаем:

Таким образом,

Но

что противоречит предыдущему равенству. Тем самым, сфера касается грани Аналогично она касается грани что завершает доказательство.