Отношение отрезков в стерео: подобие, Фалес, Менелай
Ошибка.
Попробуйте повторить позже
Через вершину тетраэдра
проведена плоскость, касательная к описанной около него сфере. Докажите, что линии пересечения
этой плоскости с плоскостями граней
и
образуют шесть равных углов тогда и только тогда, когда
Подсказка 1
Задача прям и намекает рассмотреть проекцию картинки на плоскости ABC, ACD и ABD. Что получается при проекциях? Выпишите какие-то равенства. Как их связать с вопросом задачи?
Подсказка 2
В сечениях образуется касательная к окружности, у такой прямой понятное направление, поэтому разумно провести плоскость, параллельную касательной плоскости и пересекающую грани тетраэдра, тогда получаются вписанности. Что вы можете сказать про три точки пересечения плоскости с ребрами?
Подсказка 3
Докажите, что тождество из вопроса задачи и равенство углов из условия равносильны правильности треугольника в сечении параллельной плоскостью. Для этого вам может помочь степень точки или подобие.
Проведем плоскость, параллельную касательной плоскости, пересекающую ребра
и
в точках
и
соответственно.
Рассмотрим плоскость Заметим, что
(по теореме об угле между касательной и хордой), а
(как накрест лежащие при параллельных и секущей), т. е.
Следовательно,
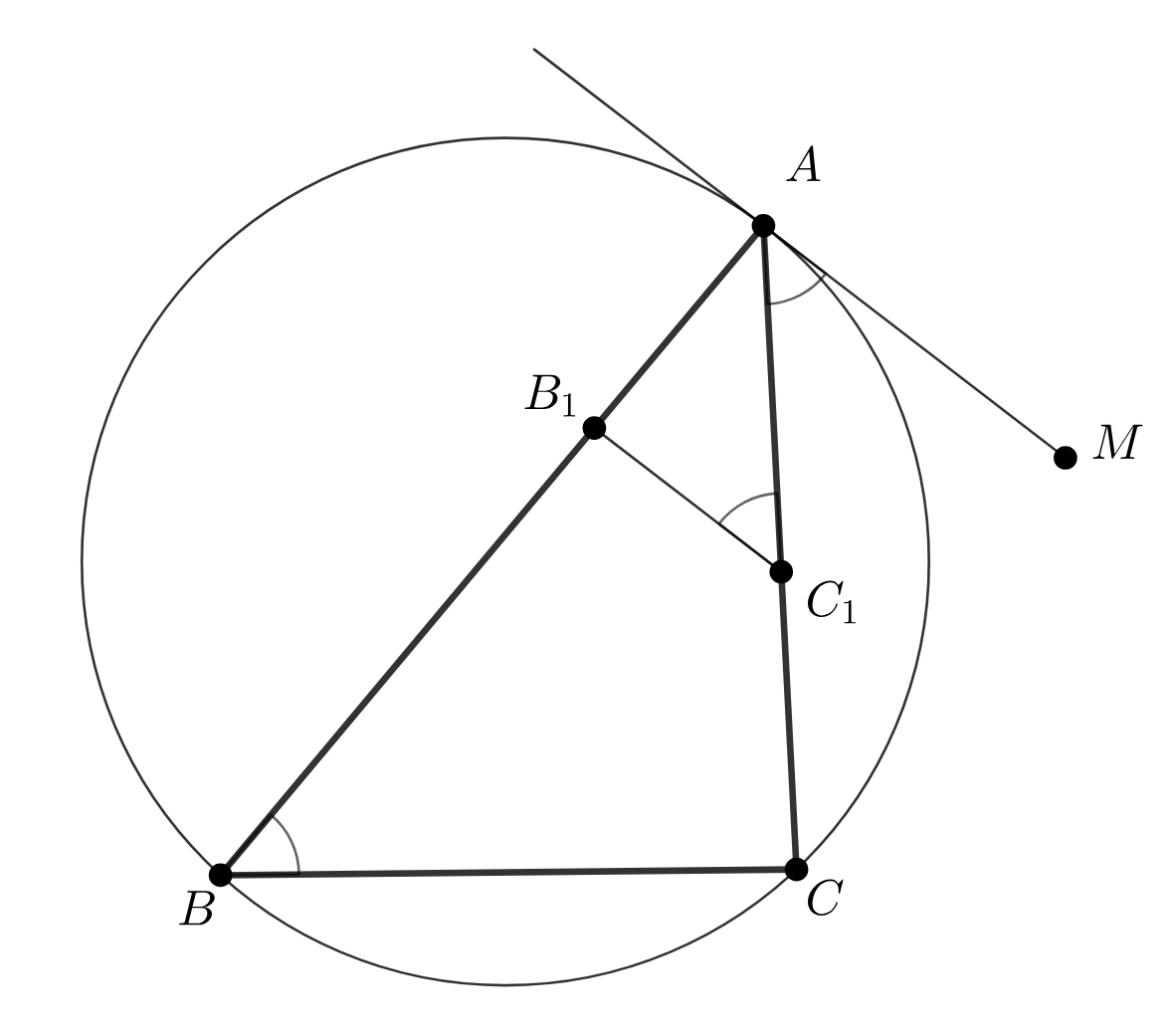
Откуда
Аналогично,
Из этих равенств вытекает, что
Значит, равносторонний тогда и только тогда, когда
Осталось заметить, что углы, образуемые указанными в условии линиями пересечения, соответственно равны углам треугольника
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




