Конус

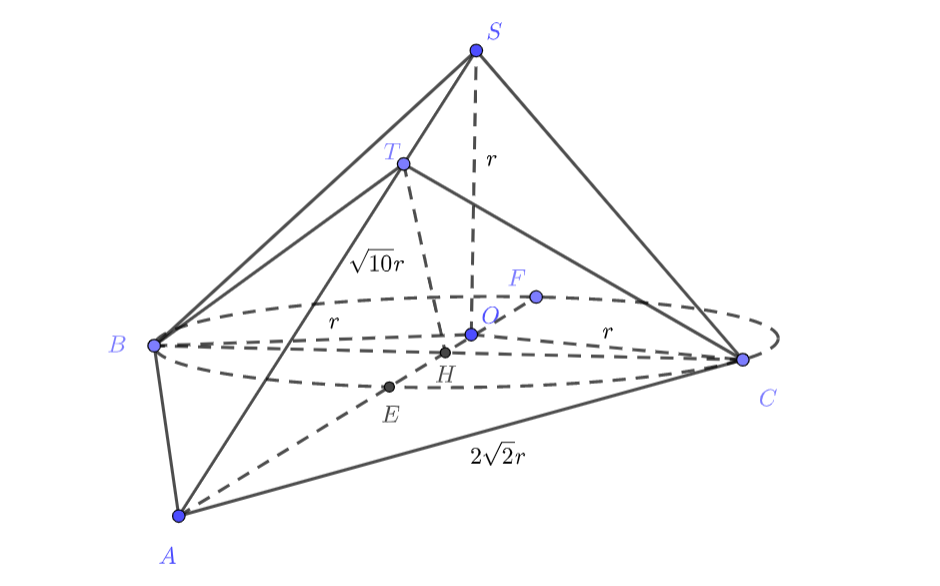
Пусть центр основания радиуса — точка , точка рядом , а — вершина конуса. Пусть также пересекает окружность в . Касательные плоскости содержат касательные из к окружности, пусть это и . Легко видеть, что и и есть искомые плоскости, проведём в этих треугольниках высоты к , которые в силу симметрии упадут в одну точку . Тогда наша задача сводится к поиску .

Итак, будем искать отрезки и . По теореме об отрезках касательной и секущей

Здесь мы просто посчитали площадь прямоугольного треугольника двумя способами. Теперь заметим, что , поскольку две прямые ей перпендикулярны, откуда , то есть , как прямоугольные с общим углом. Имеем

В итоге .