Пирамиды с общим трёхгранным углом и/или высотой
Ошибка.
Попробуйте повторить позже
На ребре основания треугольной пирамиды
расположена точка
так, что
. Через середину ребра
основания пирамиды проведена плоскость
, проходящая через точку
и параллельная боковому ребру
. В каком отношении
плоскость
делит объем пирамиды?
Источники:
Подсказка 1
Давайте для начала построим сечение плоскостью P нашей пирамиды.
Подсказка 2
Пользуясь параллельностью, мы сможем из подобия найти, в каком отношении плоскость P делит рёбра пирамиды, а значит мы сможем найти и...
Подсказка 3
Как относятся высоты маленьких пирамидок и высотам из точек A и D пирамиды ABCD.
Подсказка 4
Нам достаточно найти, какую часть объёма всей пирамиды ABCD составляет объём многогранника, лежащего со стороны вершины A. Чтобы найти его объём, можно...
Подсказка 5
Разбить его на две пирамидки. А объём каждой из них мы сможем выразить через объём всей пирамиды ABCD, потому что знаем отношения высот и отношения площадей оснований.
Построим сечение. Поскольку секущая плоскость параллельна ребру , она пересечет плоскость
по прямой
, параллельной
, а плоскость
— по прямой
, также параллельной
. Соединим точки
и
, лежащие в одной плоскости, и точки
и
, лежащие в одной плоскости, получим
— искомое сечение.
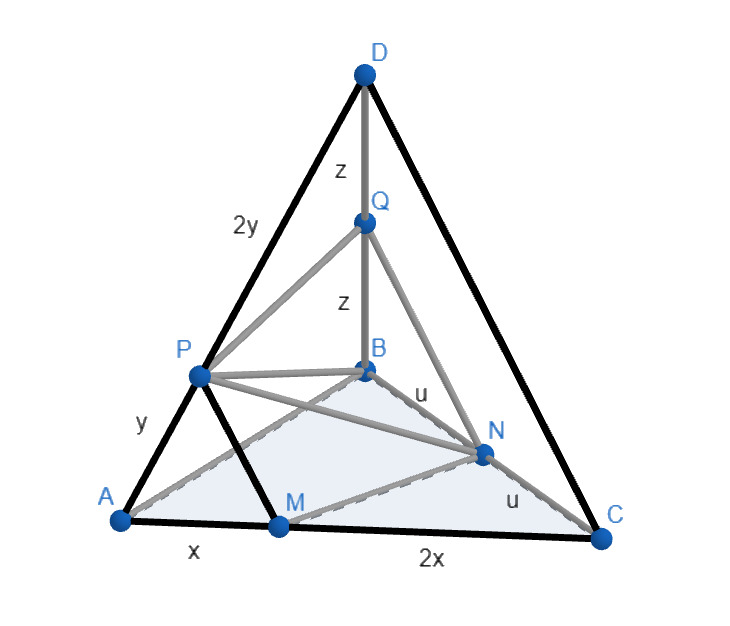
Пусть — объем пирамиды,
— сумма объемов пирамид
и
и
.
Из подобия пар треугольников и
и из условия задачи получим, что
Отсюда следует, что
где — высота, опущенная из вершины
пирамиды
,
— высота, опушенная из вершины
пирамиды
.
А также значит, что площадь основания пирамиды равна:
Тем самым:
Аналогично из подобия пар треугольников и
и из условия задачи получим, что
Отсюда следует, что
где — высота, опущенная из вершины
пирамиды
,
— высота, опущенная из вершины
пирамиды
.
А также значит, что площадь основания пирамиды равна:
Тем самым:
Теперь можно записать, что
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




