Случаи расположения точек

Обозначим искомый треугольник — середина на . Пусть — середина , тогда — высота треугольника.

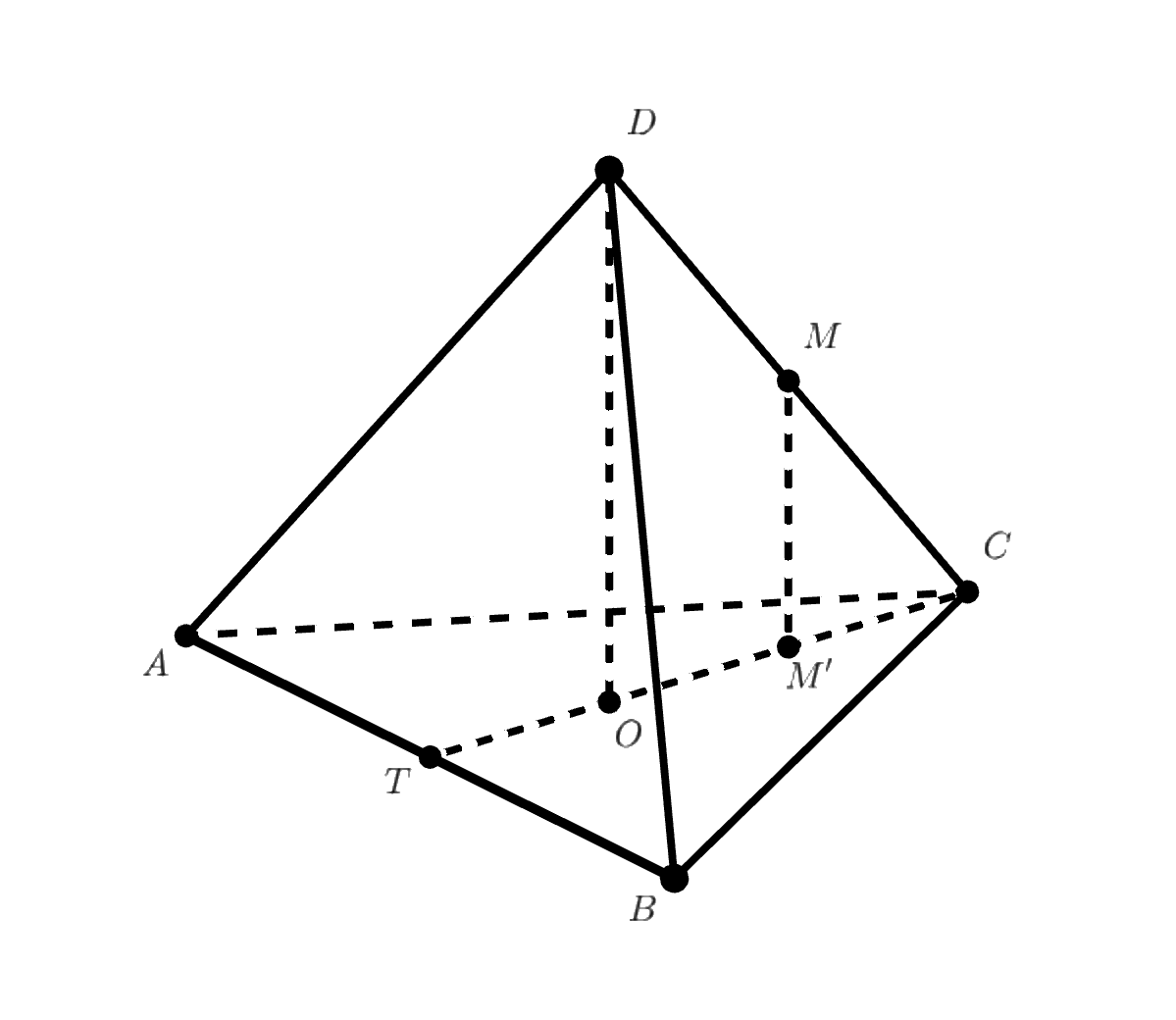
Если — проекция на высоту треугольника , то по теореме Фалеса равна половине , где — проекция и одновременно центр описанной окружности (потому что боковые рёбра пирамиды равны), то есть равна половине радиуса описанной около ABC окружности. По теореме синусов , тогда

, а

,

тем самым

Поскольку , то по теореме Пифагора

Возможны случаи:

1) .

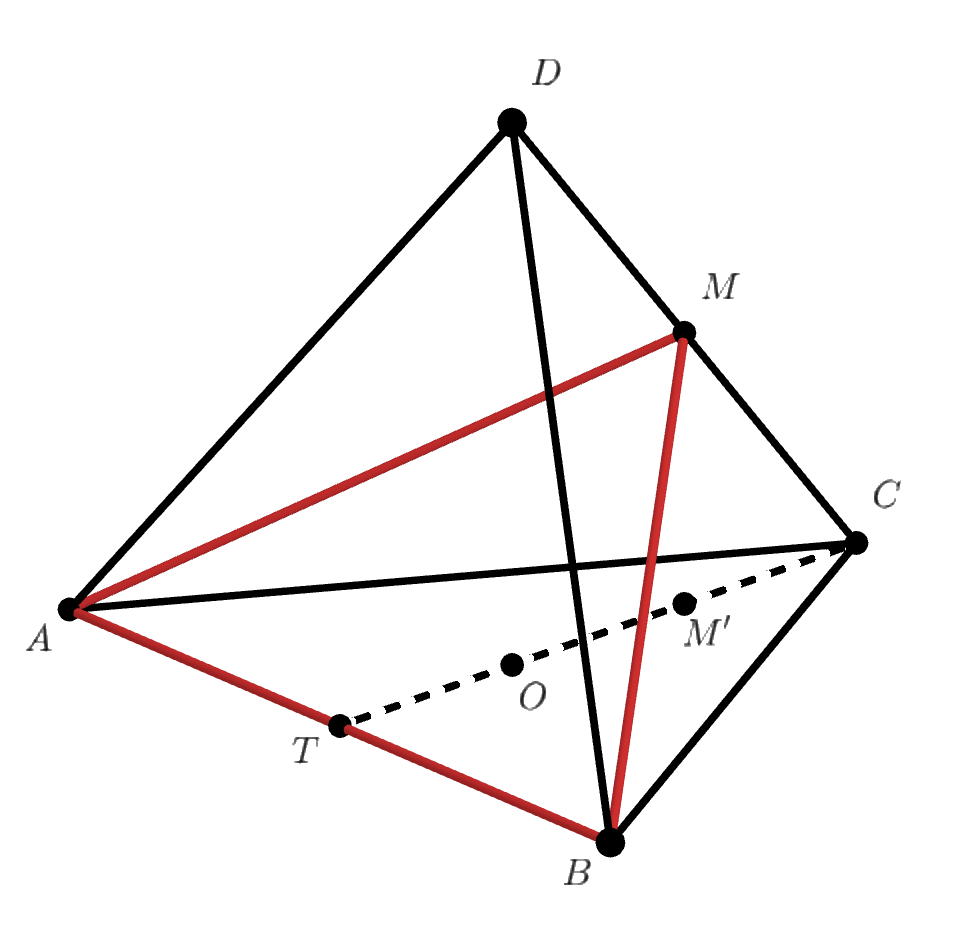
В этом случае совпадает с , поскольку пирамида симметрична относительно плоскости, проходящей через середину и перпендикулярной . Тогда

2) .

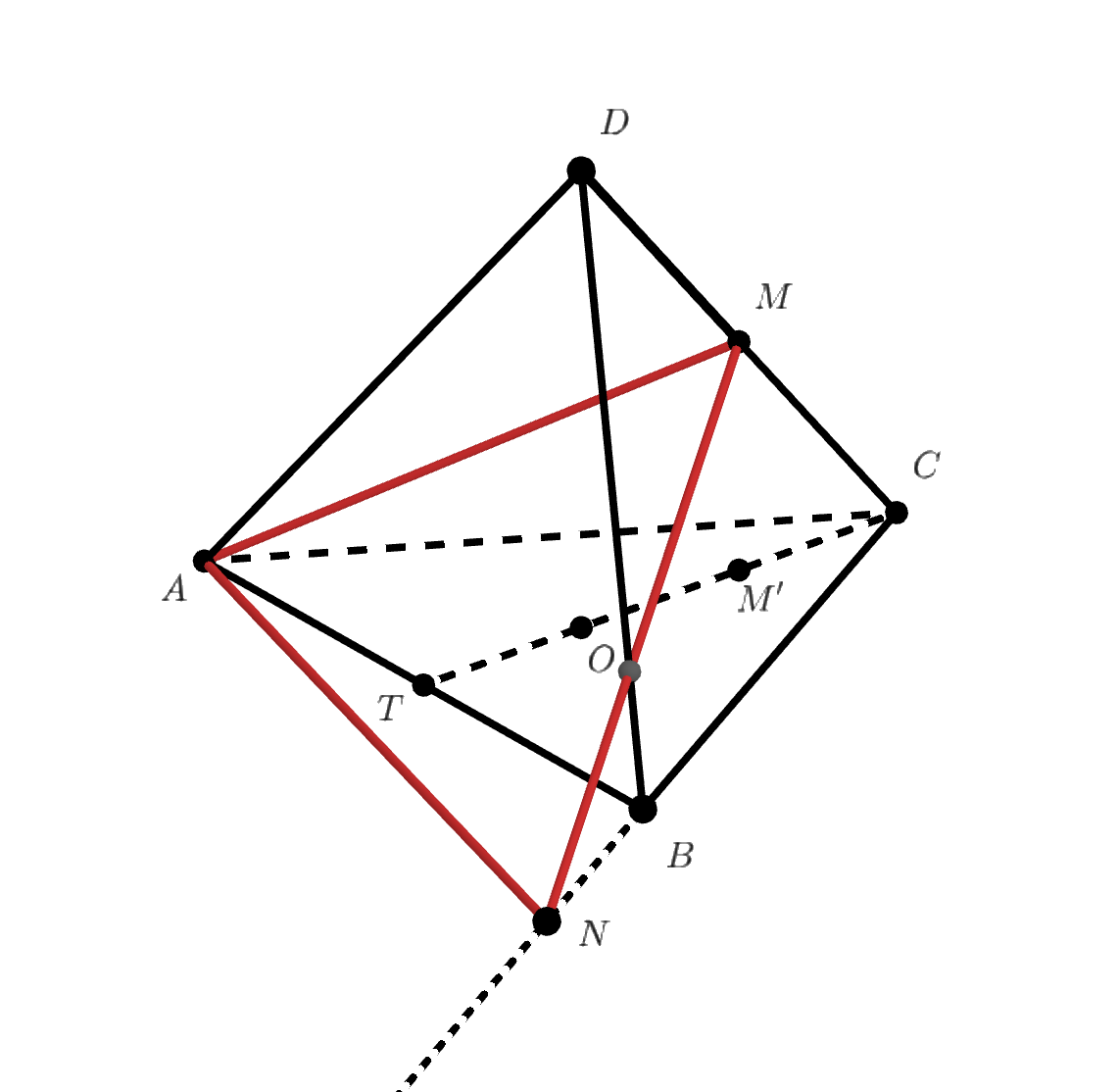
Но тогда . Но тогда точка лежит вне отрезка , иначе расстояние от до неё было бы не больше длины стороны треугольника .

3) .

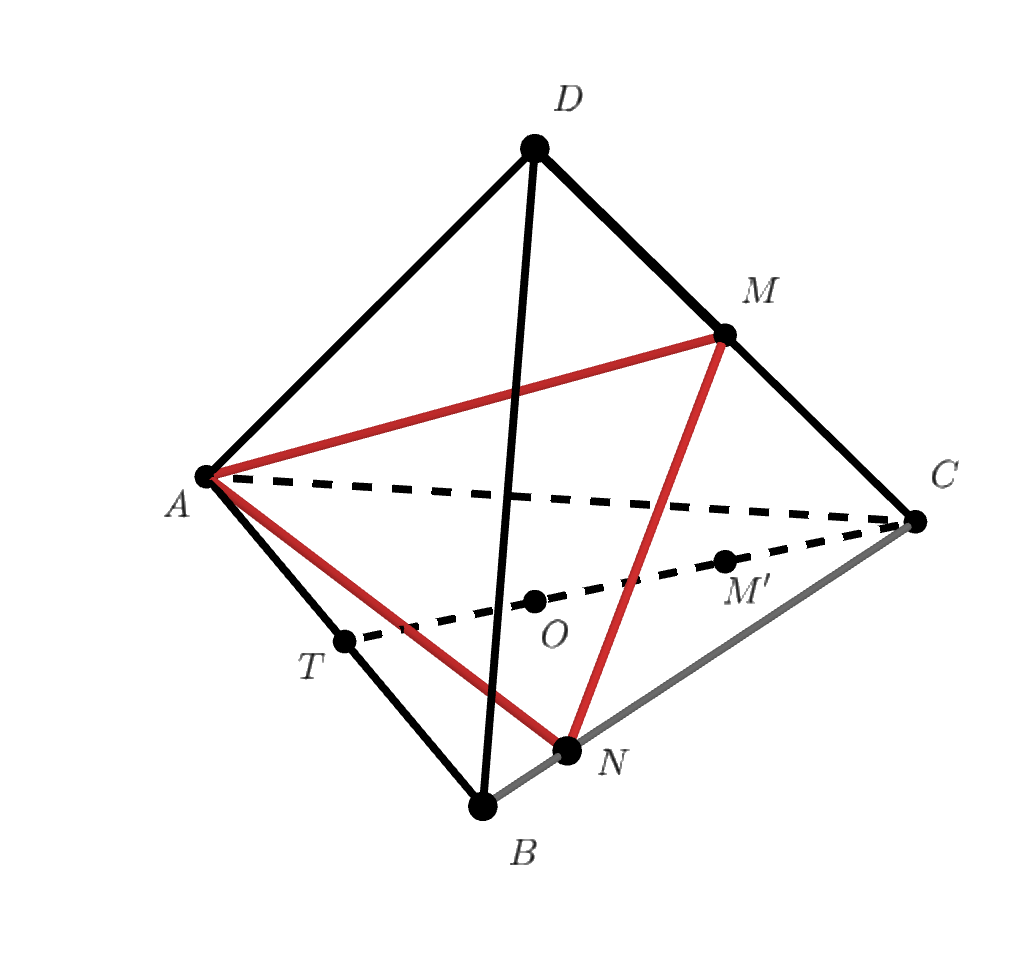
Заметим, что . Пусть , запишем теоремы косинусов для и , выберем из первого , а из второго в качестве противолежащих сторон, откуда

Подставляя в теорему косинусов, получаем . Посчитаем высоту из вершины в треугольнике с учётом

Тогда