Введение целевой функции
Ошибка.
Попробуйте повторить позже
По диагоналям оснований и
куба
с ребром
ползут два муравья Гоша и Леша. Движение они начали
одновременно из точек
и
соответственно с постоянной скоростью, причем скорость Леши была в два раза больше скорости
передвижения Гоши и закончили, когда Леша оказался в точке
. Какое наименьшее расстояние разделяло Гошу и Лешу во время
движения?
Источники:
Подсказка 1
Начинаем, как и любую геометрию, с чертежа! Обозначим на рисунке, где находился каждый из муравьёв в момент, когда их расстояние было наименьшим, а также проведём искомое расстояние. Какие неизвестные тут понадобится ввести?
Подсказка 2
Конечно же, нам понадобятся время и скорость. Призываем на помощь Пифагора, чтобы выразить искомое расстояние через имеющиеся данные! Но как же найти минимум этой функции? Что здесь переменная, а что — параметр?
Подсказка 3
Скорость зафиксирована, длина ребра куба дана в условии, а вот время t меняется по ходу движения, поэтому будем смотреть на нашу функцию от переменной t! Какой вид имеет квадрат расстояния? Где у такой штуки минимум?
Подсказка 4
Перед нами квадратный трёхчлен, его минимум мы умеем искать, но важно проверить, не будет ли расстояние, которое прошли муравьи к моменту, соответствующему вершине параболы, превышать длину диагонали? Сделайте выводы и запишите ответ! Если всё посчитано верно, то параметр скорости сократится! ;)
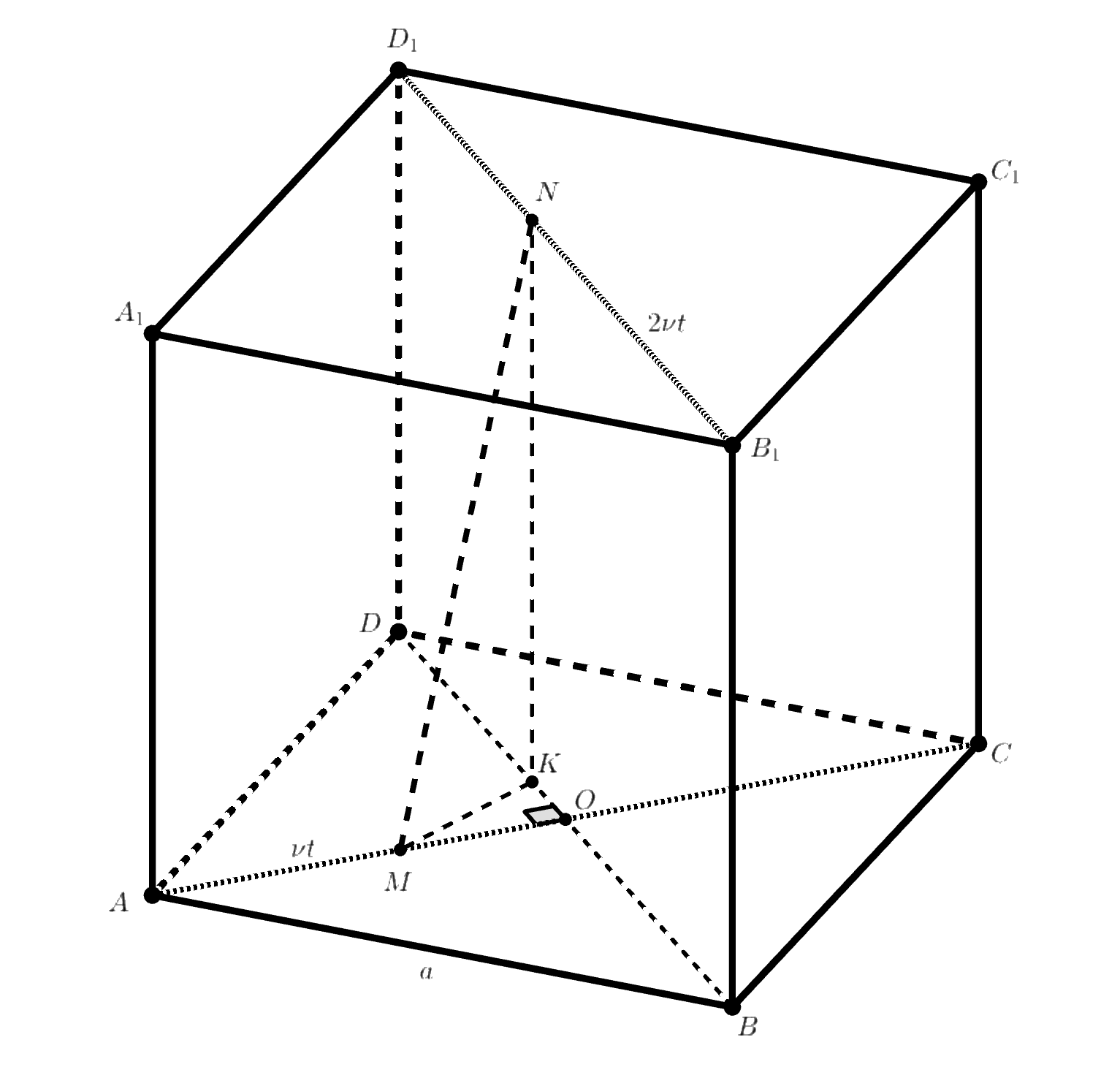
Фиксируем момент времени
— положение муравьёв в момент
— проекция точки
на диагональ
— скорость движения Гоши,
— скорость Леши.
Тогда имеем
Наконец,
Движение закончилось, когда последняя скобка занулилась, то есть при Относительно
функция
является квадратным
трёхчленом с положительным коэффициентом при
Вершина находится в точке
Отсюда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




