Муниципалка 10 - 11 класс
Ошибка.
Попробуйте повторить позже
Некоторые клетки доски отмечены. Назовем клетки соседними, если они имеют общую сторону. Оказалось, что у каждой клетки
есть, по крайней мере, один отмеченный сосед. Доказать, что есть клетка, у которой, по крайней мере, два отмеченных
соседа.
Источники:
Подсказка 1
Нужно придумать раскраску, которой мы красиво сможем покрыть нашу доску. Предположим противное. Понятно, что для любой раскрашенной клетки существует ровно одна отмеченная рядом. Какую раскраску можно придумать, чтобы одна отмеченная клетка соответствовала двум раскрашенным?
Подсказка 2
Раскрасим диагонали в каждом квадрате 11*11. Скольким раскрашенным клеткам должна соответствовать каждая отмеченная клетка? Осталось лишь найти противоречие с нашей раскраской ;)
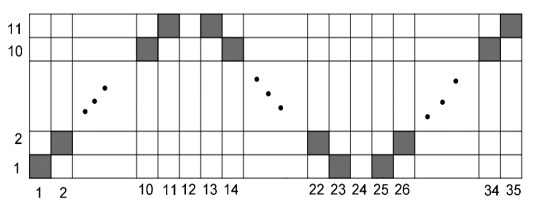
Раскрасим диагонали в каждом квадрате , как на рисунке выше. Мы покрасили
клетки и для каждой из них должна быть
ровно одна отмеченная рядом. Заметим, что любая соседняя для любой раскрашенной клетки является соседней ещё для
ровно одной раскрашенной, то есть любой сосед будет общим для каких-то двух раскрашенных клеток. Но раз так, то
каждая отмеченная будет ровно одна на две раскрашенные и покрашенные клетки должны разбиться на пары. Поскольку
их
, то такое невозможно и среди этих клеток найдётся хотя бы одна с хотя бы двумя отмеченными соседями, что и
требовалось.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




