Муниципалка 10 - 11 класс
Ошибка.
Попробуйте повторить позже
В выпуклом четырехугольнике на сторонах
и
расположены точки
и
соответственно. Известно, что
,
и
Докажите, что
Источники:
Подсказка 1
Множество параллельных прямых намекает нам, во-первых, на множество пар равных углов, но они нам в доказательстве мало чем могут помочь, а, во-вторых, на теорему о пропорциональных отрезках. Но если мы просто построим четырехугольник и проведем все прямые, то по такому рисунку мы не сможем применить никак теорему о пропорциональных отрезках. Подумайте, какое дополнительное построение нам необходимо для этого провести.
Подсказка 2
Давайте продлим прямые BA и CD до пересечения в точке T. Теперь мы можем записать две пропорции: AT/AP=(TD+DQ)/QC и TD/DQ=(TA+AP)/PB. Подумайте, как можно переписать то, что AB ⊥ AD, если мы знаем, что AB ⊥ BC и как нам могут помочь в дальнейшем доказательстве ранее полученные пропорции?
Подсказка 3
Для доказательства того, что AB ⊥ AD, на будет достаточно доказать, что AD параллельно ВC. Если мы перемножим пропорции крест накрест и вычтем одно выражение из второго, то получим равенство AT*DQ + AT*QC = AP*TD + BP*TD. Подумайте, почему это доказывает параллельность AD и BC.
Поскольку , то достаточно доказать
. Пусть
. Введём обозначения
.
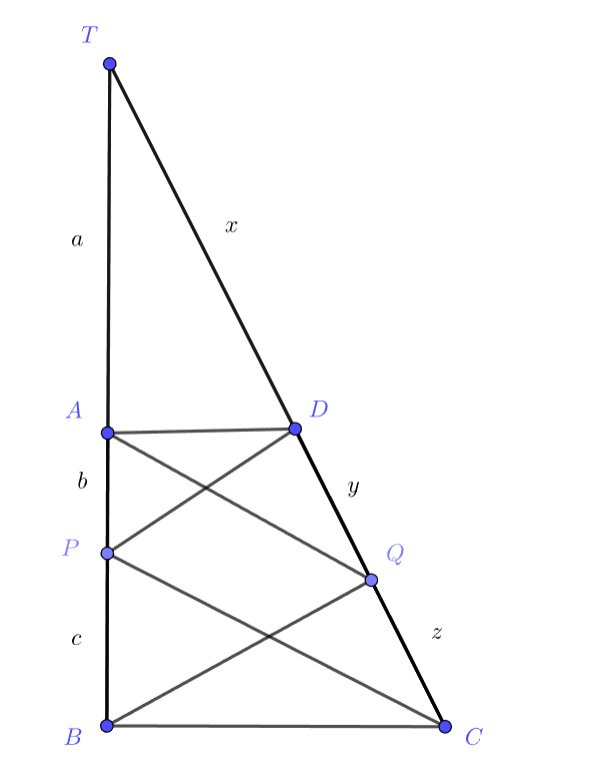
Из следует
Аналогично из
Нам же требуется показать
Остаётся заметить, что это равенство является разностью двух равенств выше.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




