ГМТ, расположение объектов в пространстве
Ошибка.
Попробуйте повторить позже
На поверхности тетраэдра 
нашлись такие точки 
и 
что 
и 
Докажите, что
Пусть 
и 
— параллельные плоскости, содержащие ребра 
и 
обозначим через 
расстояние между этими плоскостями. Ясно,
что 
С другой стороны, из условия следует, что точки 
и 
лежат как в плоскости, перпендикулярной 
и проходящей
через середину 
так и в плоскости, перпендикулярной 
и проходящей через середину 
(эти плоскости различны, так как
прямые 
и 
не параллельны). Тогда 
— линия пересечения этих плоскостей, поэтому прямая 
перпендикулярна
плоскостям 
и 
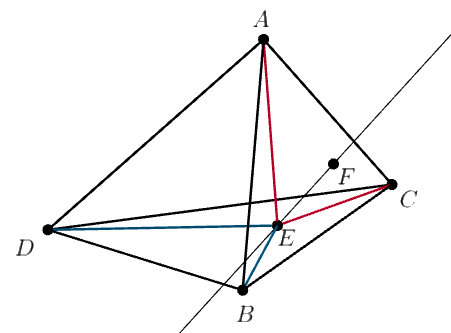
Кроме того, поскольку 
и 
лежат на поверхности тетраэдра, то обе эти точки лежат в полосе между 
и 
Значит,
что и требовалось.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
