ГМТ, расположение объектов в пространстве

Обозначим через точку пересечения боковых сторон трапеции Тогда точка является центром гомотетии с положительным коэффициентом, переводящей отрезок в отрезок По теореме о трех центрах гомотетии (теорема о трёх колпаках) точки лежат на одной прямой. Обозначим эту прямую через и докажем, что все такие прямые лежат в одной плоскости.

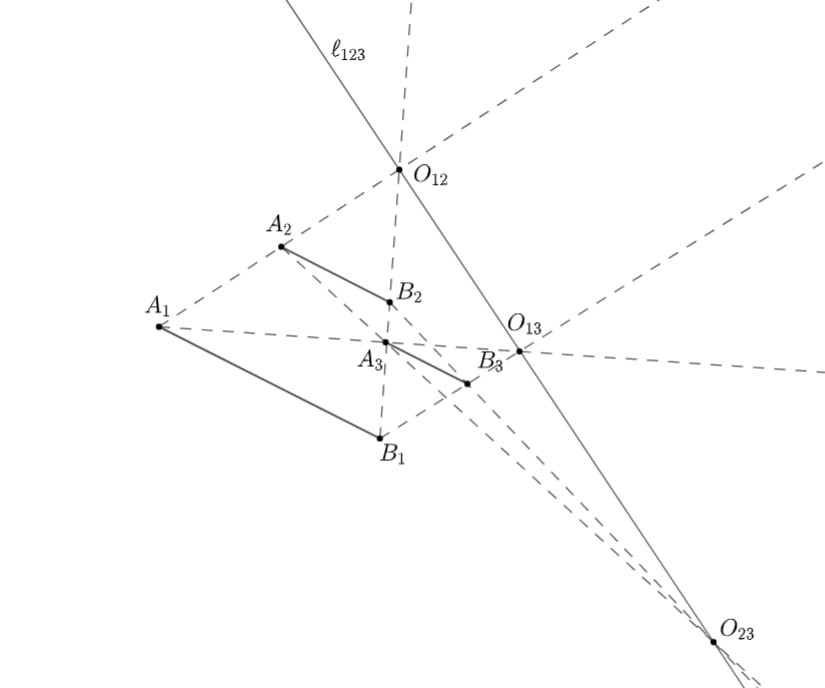
Для этого будем последовательно рисовать их. Сначала проведем прямые и они лежат в одной плоскости т.к. пересекаются в точке Прямая пересекает в точке а прямую — в точке поэтому она также лежит в плоскости Наконец, прямая пересекает прямую в точке а прямую — в точке так что и она лежит в плоскости

Итак, все четыре прямые лежат в одной плоскости, и в ней же лежат все шесть точек что и требовалось доказать.