ГМТ, расположение объектов в пространстве
Ошибка.
Попробуйте повторить позже
Дан отрезок Точки
в пространстве выбираются так, чтобы
был правильным треугольником, а
– квадратом.
Докажите, что ортоцентры всех получающихся таким образом треугольников
попадают на некоторую фиксированную
окружность.
Источники:
Подсказка 1
Что мы имеем? Равносторонний треугольник — симметричная фигура, квадрат тоже крут в этом плане. Может быть тогда треугольник XYZ имеет похожие свойства?
Подсказка 2
Попробуйте доказать, что треугольник XYZ — равнобедренный. Как же это сделать? Ну, например, можно честно, рас писать равенства сторон и так далее. Либо же воспользоваться прекрасным преобразованием — симметрией.
Подсказка 3
Отметим серединки AB и ZY — M, N соответственно, рассмотрим плоскость NMX, скажем пару волшебных слов и готово:) Что же дальше?
Подсказка 4
Треугольник XYZ — равнобедренный. Что тогда можно сказать про его ортоцентр?
Подсказка 5
Он лежит на XN — серпере к YZ. Уже неплохо:) Ключевая идея в подобных задачах: угадать окружность или сферу (от задачи зависит), но изредка, прям редко, может быть иначе (не стоит об этом забывать). Итак, хотим угадать сферу. Всё так симметрично относительно плоскости XMN. Кажется, стоит искать эту окружность в этой плоскости. Теперь, следующее понимание: весь сюжет вращается вокруг AB, кажется, что центр искомой окружности тоже лежит на нём. Итак, что мы имеем?
Подсказка 6
Гипотеза: центр искомой окружности — точка M. Что же делать с радиусом? Угадать бы какую-нибудь точку окружности было бы славно. Как же это можно делать? Ну, например, рассмотреть экстремальные случаи. Ну, советую рассмотреть случай, когда квадрат и треугольник в одной плоскости (ну и там уже можно координатно или в синусах посчитать, или в теорема Пифагора)
Подсказка 7
Так или иначе вы доказали, что одно из положений ортоцентра — это точка X. Теперь хотим в общем виде доказать, что все ортоценты лежат на окружности с центром в M и радиусом MX. Теперь подумаем, как же это сделать? Для этого стоит отметить точки S, T на прямой MN по обе стороны от M так, чтобы MS = MT = MX (T на отрезке MN). Как быть дальше?
Подсказка 8
Считать уголки — так себе идея... Но что мы еще умеем делать, чтоб доказывать вписанность?
Подсказка 9
Степень точки! Самой приятной кажется точка N. То есть осталось доказать, что NT*NS = NH*NX, где H — ортоцентр XYZ. Теперь пусть AB = a. Осталось написать пару теорем Пифагора, немного повыражать и доказать равенство, а как следствие, и решение задачи у нас в кармане)
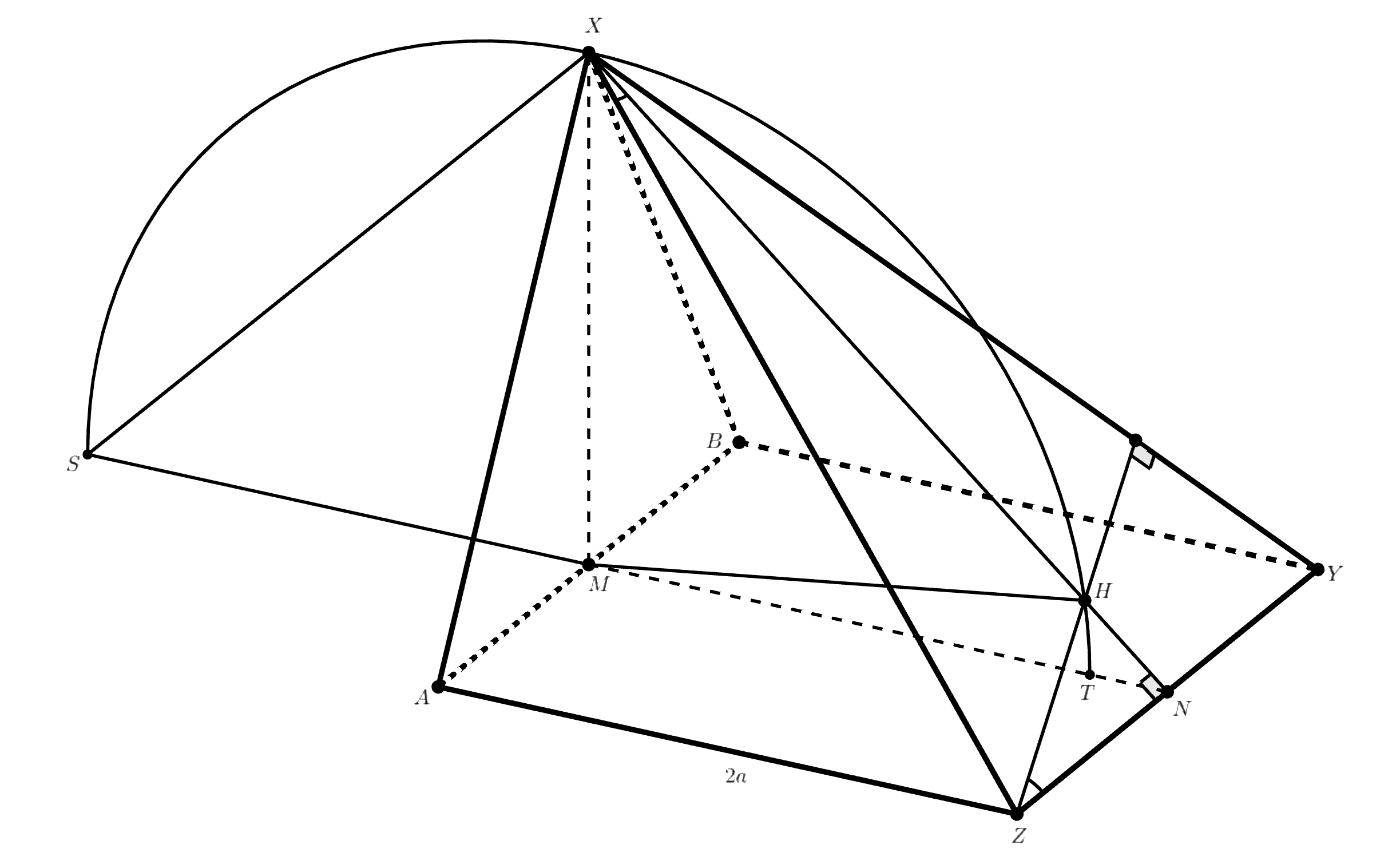
Пусть — середина
— середина
Рассмотрим плоскость
Заметим, что прямая
перпендикулярна прямым
и
а значит она перпендикулярна плоскости
Следовательно,
Нетрудно видеть, что при симметрии
относительно плоскости
отрезок
перейдёт в отрезок
то есть
Таким образом, ортоцентр
треугольника
лежит на отрезке
— серединном перпендикуляре
Покажем, что лежит на окружности
с центром
радиусом
лежащей в плоскости
Для этого определим на
отрезке
точку
такую, что
и точку
— вторичное пересечение прямой
с
Осталось посчитать, что
четырёхугольник
— вписанный, то есть доказать равенство
Пусть длина стороны квадрата и правильного треугольника равна Из подобия треугольников
и
нетрудно получить,
что
Также понятно, что
откуда Получили нужное равенство.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




