.03 Уравнение гармонических колебаний
Ошибка.
Попробуйте повторить позже
На гладком столе стоит коробка массой (см. рисунок). В коробке находятся два бруска, масса каждого из которых
также равна
. Трения в системе нет. Левый брусок соединён с коробкой лёгкой горизонтальной пружиной жёсткостью
. Правому бруску сообщили скорость
в направлении левого бруска. При столкновении бруски слипаются и движутся
дальше как одно целое. Найдите максимальную скорость коробки и максимальное сжатие пружины при дальнейшем
движении.
(МОШ, 2009, 11)

Источники:
По закону сохранения импульса слипшиеся грузы скользят со скоростью
Заменим системы на равносильную
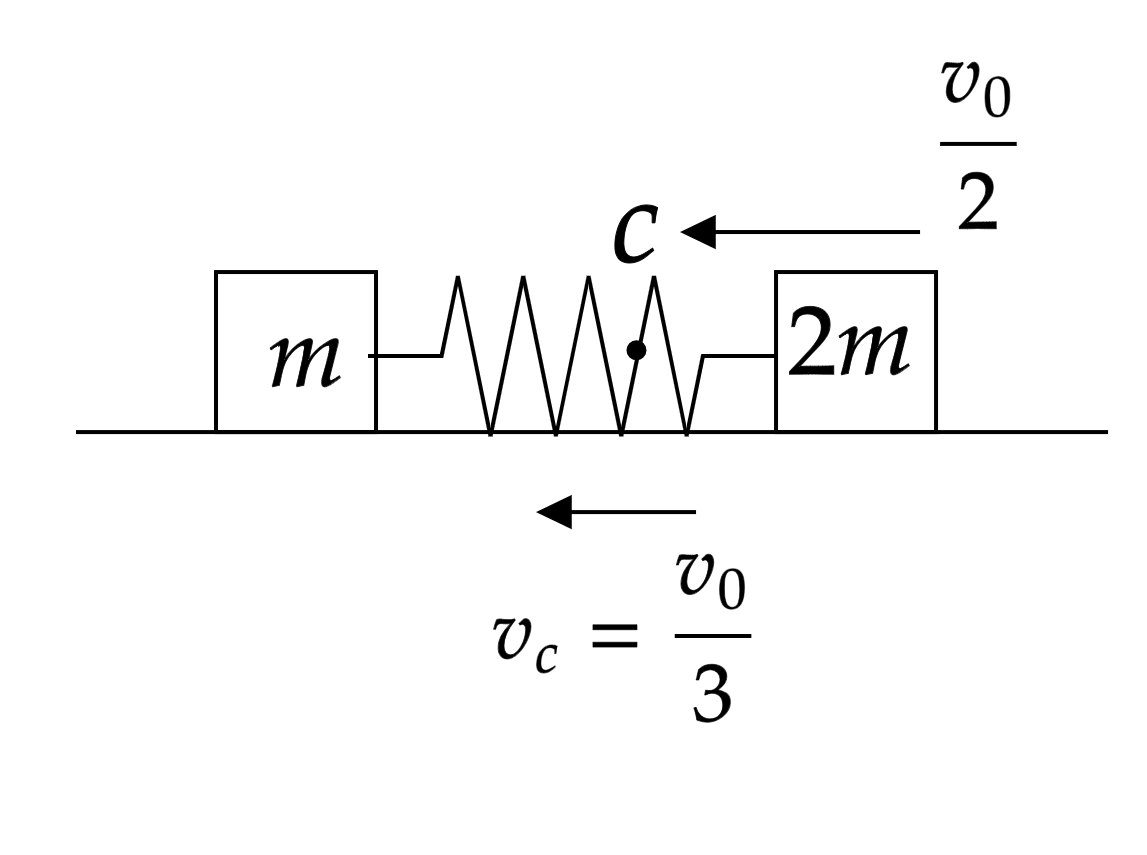
Так как на систему не действуют внешние силы, то скорость центра масс постоянна
Пусть начальная длина пружины равна , тогда центр масс находится на расстоянии
от
и
от
.
Перейдем в ИСО, связанную с центром масс.
Рассмотрим колебания каждого груза относительно центра масс оба бруска будут двигаться по гармоническому закону с
циклической частотой
где жесткость пружины длиной
(
), а
жесткость пружины длиной
(
).
Циклическая частота равна
Колебания происходят по законам
где и
– смещение от начального положения грузов.
Тогда скорости меняются по законам
Откуда
Окончательно законы колебаний выглядят следующим образом:
Максимальная скорость , тогда в лабораторной системе отсчета
Так как сжатие пружины максимально, то относительная скорость грузов равна 0, то есть
По закону сохранения импульса
А из закона сохранения энергии
Тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




