.03 Уравнение гармонических колебаний

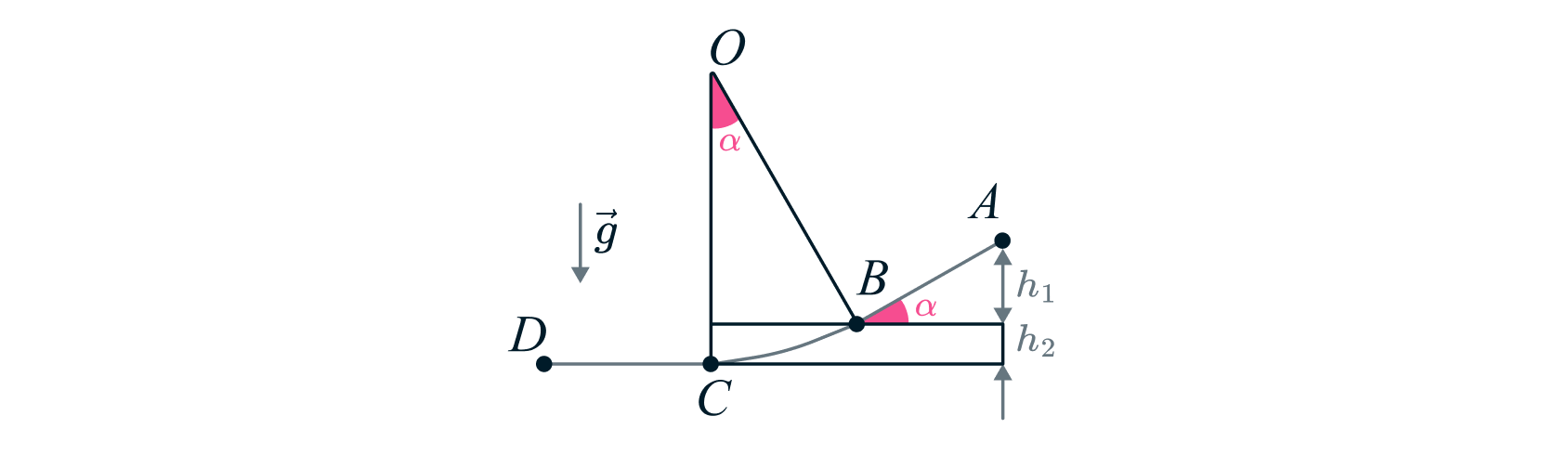
Полное время движения муравья складывается из времени движения по участку , времени на участке и времени на участке . Пусть .
1. Восстановим из точек и перпендикуляры к траектории движения муравья, они являются радиусами дуги (рис. ). Пусть . Поскольку , то . Ускорение на прямолинейном участке равно . Тогда

Скорость в конце этого участка

2. Вычислим . Из закона сохранения энергии найдем скорость муравья в точке . Это будет его наибольшая скорость.

Найдем :

Тогда

На участке движение муравья аналогично колебательному движению математического маятника с длиной подвеса . Его циклическая частота . Время движения муравья из точки в точку равно времени его обратного движения из точки в точку , которое можно найти из уравнения гармонических колебаний:

3. На отрезке муравей движется равномерно со скоростью , следовательно,

Полное время движения муравья:

(Официальное решение ВсОШ)