.03 Уравнение гармонических колебаний
Ошибка.
Попробуйте повторить позже
Однородный прямоугольный брусок скользит со скоростью 
, направленной вдоль его более длинных сторон (длиной
), по гладкой горизонтальной поверхности. В некоторый момент времени он встречает границу очень
обширной шероховатой области, перпендикулярную направлению его движения. За какое время после этого он
остановится? Считать, что сила трения для части бруска пропорциональна площади этой части. Известно, что
если скорость 
сообщить бруску, покоящемуся внутри шероховатой области, то он остановится за время
.
(«Покори Воробьёвы горы!», 2017, 10–11)
Источники:
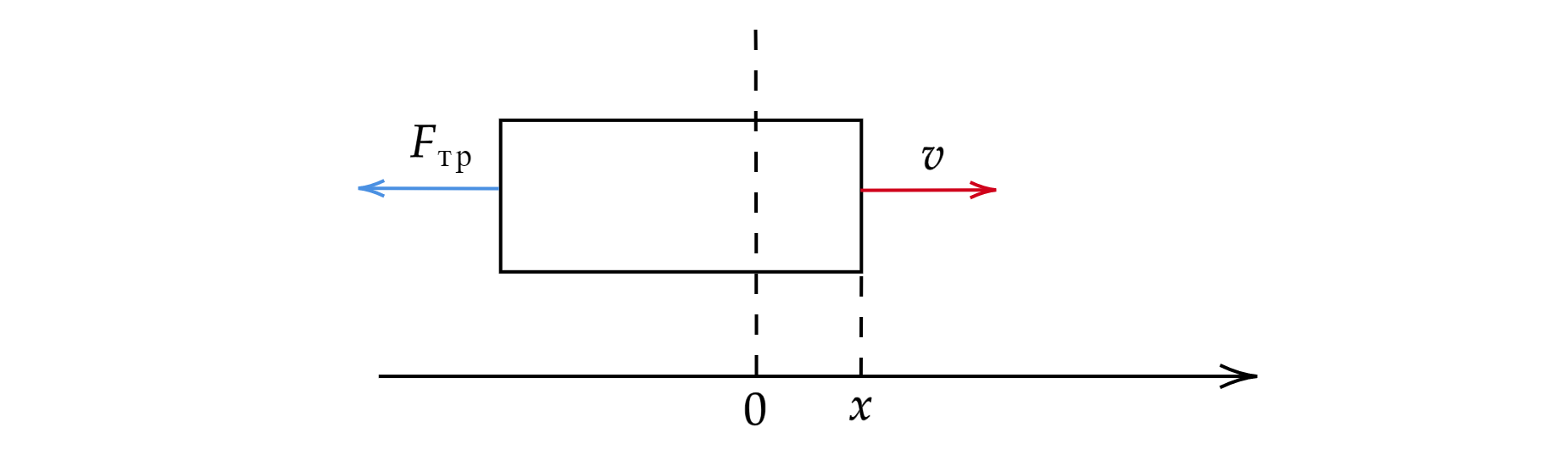
Знание времени торможения бруска на шероховатой горизонтальной поверхности позволяет определить коэффициент
трения 
: поскольку сила трения сообщает бруску ускорение, равное по модулю 
и направленной против скорости, то
Запишем теперь уравнение движения бруска массой 
в процессе пересечения границы шероховатой
области:
Как видно, брусок будет двигаеться по гармоническому закону
С учетом начальных условий 
, 
, получаем закон движения переднего края бруска
 |
и закон изменения скорости бруска 
. Поскольку у нас 
то брусок полностью
пересечет границу за время 
, определяемое из соотношения
и его скорость в этот момент времени будет равна 
Далее брусок тормозит с
постоянным ускорением, и его скорость уменьшается до нуля
В результате полное время торможения
(Официальное решение ПВГ)
| Критерии оценивания выполнения задачи | Баллы |
| Сделан верный вывод о значении | 2 |
| Получен закон движения переднего края бруска | 2 |
| Получено значение времени | 2 |
| Получено значение времени | 2 |
| Получен верный численный ответ | 2 |
| Максимальный балл | 10 |
, за которое брусок полностью пересечет границу 
, за которое брусок тормозит с постоянным ускорением до полной остановки 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
