.03 Уравнение гармонических колебаний

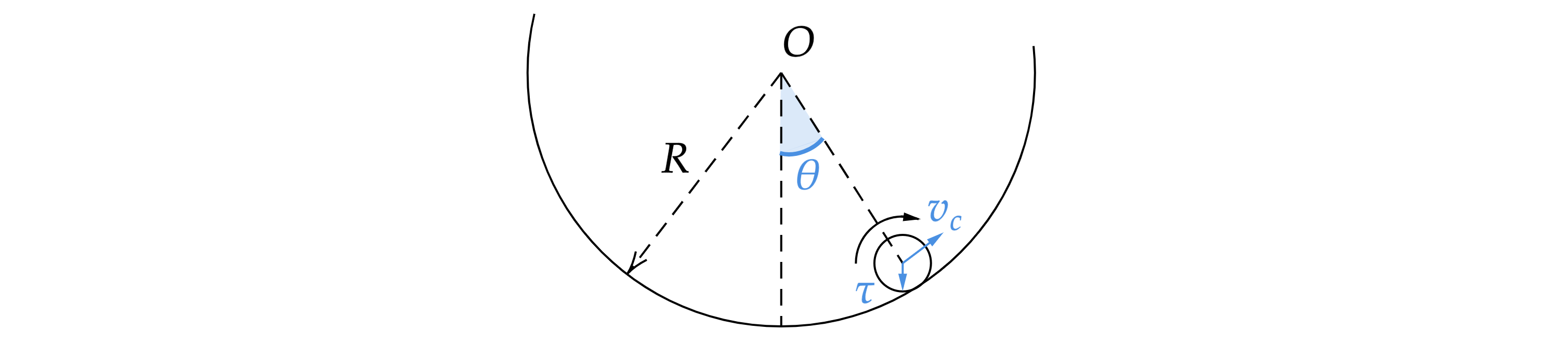
Рассмотрим цилиндр, когда он смещается из своего устойчивого положения равновесия на малый угол во время колебаний (рис.). Если – мгновенная скорость центра масс () цилиндра, то его угловая скорость вокруг собственного центра равна

Так как движется по кругу радиуса (), скорость в тот же момент может быть записана

Таким образом, из (1) и (2)

Поскольку механическая энергия колебаний твердого цилиндра сохраняется, то

(Где – масса цилиндра, – момент инерции цилиндра вокруг оси, проходящей через ее центр масс (C) и перпендикулярно плоскости чертежа) или

(с использованием (1) и )

(используя уравнение 3) Дифференцируя по времени

Тогда,

(поскольку при малых , ) Таким образом

Следовательно, искомый период колебаний