.02 Колебательные системы
Ошибка.
Попробуйте повторить позже
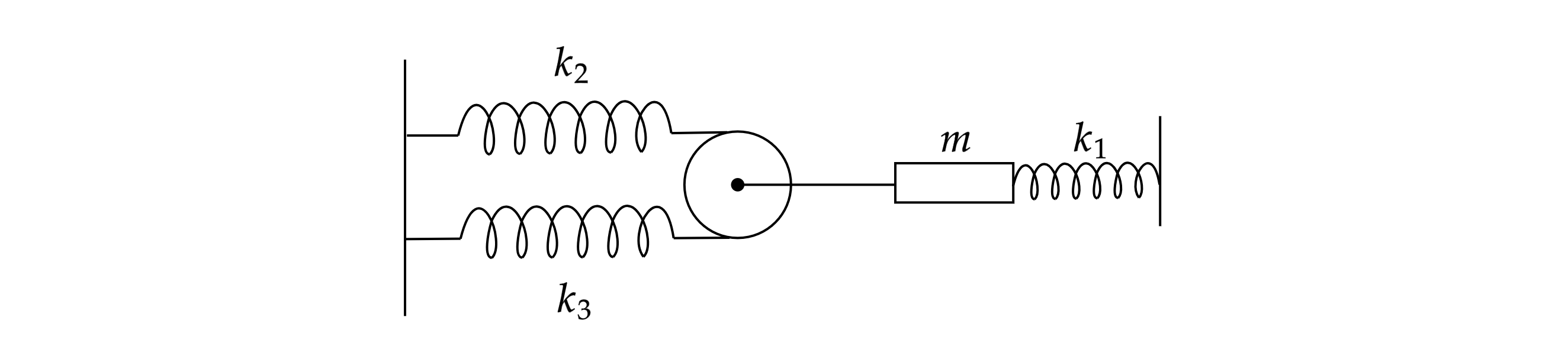
Колебательная система состоит из груза массой , лежащего на гладкой горизонтальной
плоскости, невесомого гладкого блока, двух невесомых, нерастяжимых нитей и трёх невесомых пружин
жёсткостью
,
и
, соответственно, соединённых так, как
показано на рисунке. Центр масс груза лежит на одной горизонтали с прикреплённой к нему нитью и
осью пружины
. В положении равновесия все пружины растянуты. Считая, что нити все время
остаются натянутыми, определите круговую частоту
малых гармонических колебаний груза.
(Ломоносов, 2021, отбор 11)
Источники:
Пусть растяжения пружин в положении равновесия равны ,
и
, соответственно. Тогда сила
натяжения пружины
и правой нити, прикреплённой к грузу, равна
, а сила натяжения
нити, переброшенной через блок, равна
т.к. блок гладкий. Из условия невесомости
блока следует, что
, а поэтому
При смещении груза вправо на расстояние первая пружина сократится на
, а вторая и
третья удлинятся на
и
, соответственно, причём
т.к. нити нерастяжимы и
т.к. пружины невесомы. Отсюда находим, что
Изменение потенциальной системы при этом будет
Иcпользуя записанные выше соотношения между и
, нетрудно убедиться в том, что
выражение в круглых скобках обращается в нуль. Кроме того
Следовательно,
Обозначив через скорость груза в положении равновесия, по закону сохранения механической
энергии имеем
Поскольку амплитудное значение скорости связано с амплитудой смещения
соотношением
, искомая частота
(Официальное решение Ломоносов)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




