.02 Колебательные системы
Ошибка.
Попробуйте повторить позже
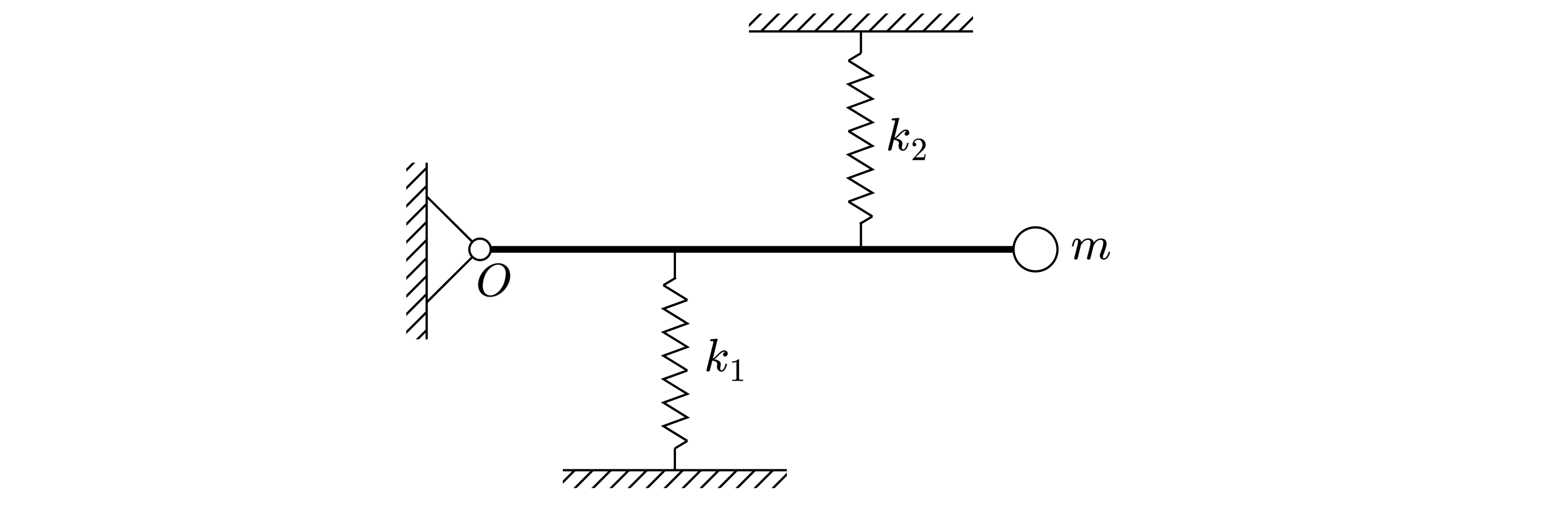
Конструкция из жёстко соединённых лёгкого стержня и небольшого шарика массой может
совершать колебания под действием двух пружин с жёсткостями
и
, двигаясь при вращении без
трения вокруг вертикальной оси
по гладкой горизонтальной поверхности стола (см. рисунок).
Пружины лёгкие, их оси горизонтальны, а точки прикрепления к стержню делят его на три равные
части. В положении равновесия оси пружин перпендикулярны стержню, и пружина с жёсткостью
растянута на величину
.
1) Найти деформацию второй пружины в положении равновесия.
2) Найти период малых колебаний конструкции.
(МФТИ, 1996)
Источники:
1) Пусть длина всего стержня , так как пружина жёсткостью
растянута, то сила упругости
направлена вниз, следовательно, для равновесия сила упругости пружины
должна быть
направлена вверх. Стержень расположен вертикально. По правилу моментов относительно точки
Момент силы тяжести равен нулю, так как стержень направлен вертикально.
2) Пусть в некоторый момент смещение шарика от положение равновесия равно
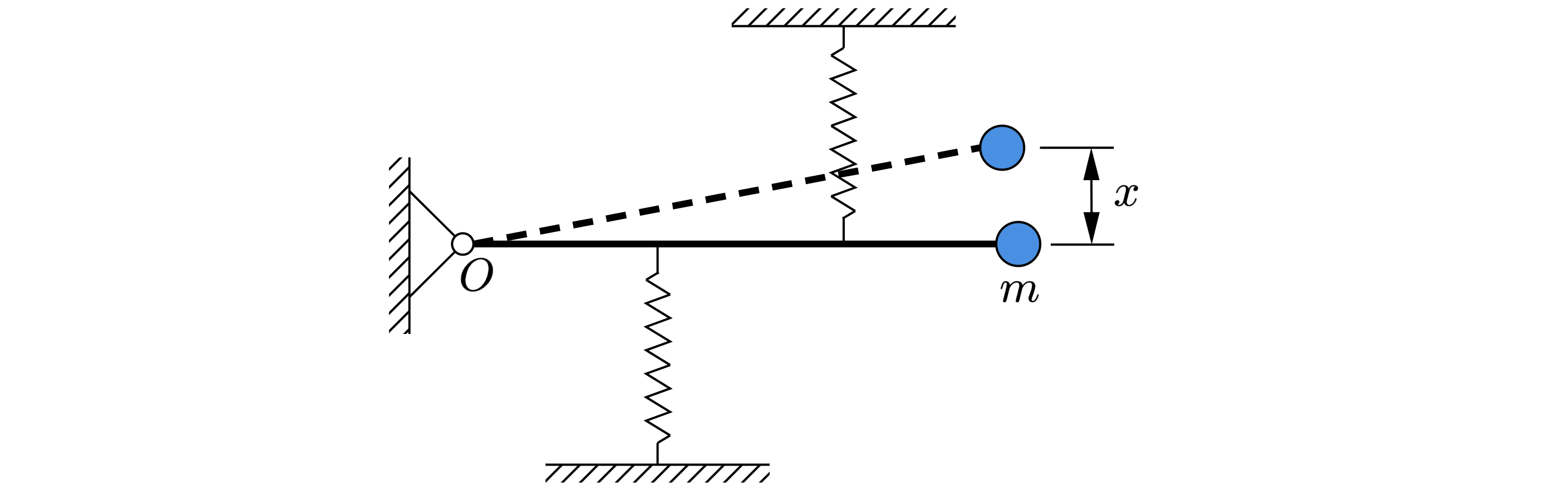
Из подобных треугольников растяжение первой пружины увеличится на , а второй уменьшится
на
. Следовательно, деформация первой пружины равна:
а второй
Потенциальная энергия каждой из пружин
Кинетическая энергия шарика
где – скорость шарика.
При гармонических колебаниях
Подставив в последнее равенство записанные выше выражения и продифференцировав полученное уравнение по времени, после упрощений получим:
Отсюда циклическая частота:
Период колебаний равен:
| Критерии оценивания выполнения задачи | Баллы |
| Записано правило моментов | 2 |
| Записана деформация первой пружины | 2 |
| Записана деформация второй пружины | 2 |
| Записан закон сохранения механической энергии | 2 |
| Представлен правильный ответ | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




