.02 Колебательные системы
Ошибка.
Попробуйте повторить позже
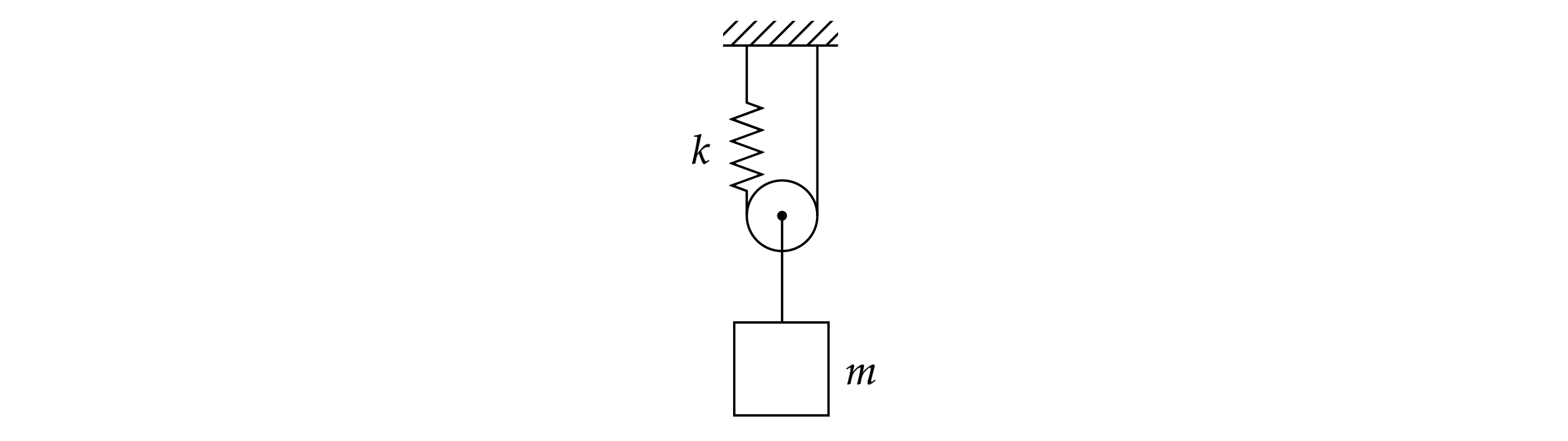
Груз массой подвешен с помощью пружины жёсткостью
, лёгких нитей и невесомого блока (см.
рисунок).
1) Найти удлинение пружины в положении равновесия системы.
2) Найти период вертикальных колебаний груза при условии непровисания нитей.
(МФТИ, 1996)
Источники:
1) Сила натяжения нити от груза равна
, после блока она ”делится на 2 участка”, значит, сила
упругости пружины:
отсюда искомая величина
2) Пусть длина недеформированной пружины , длина нити –
,
– деформация пружины.
Расставим силы
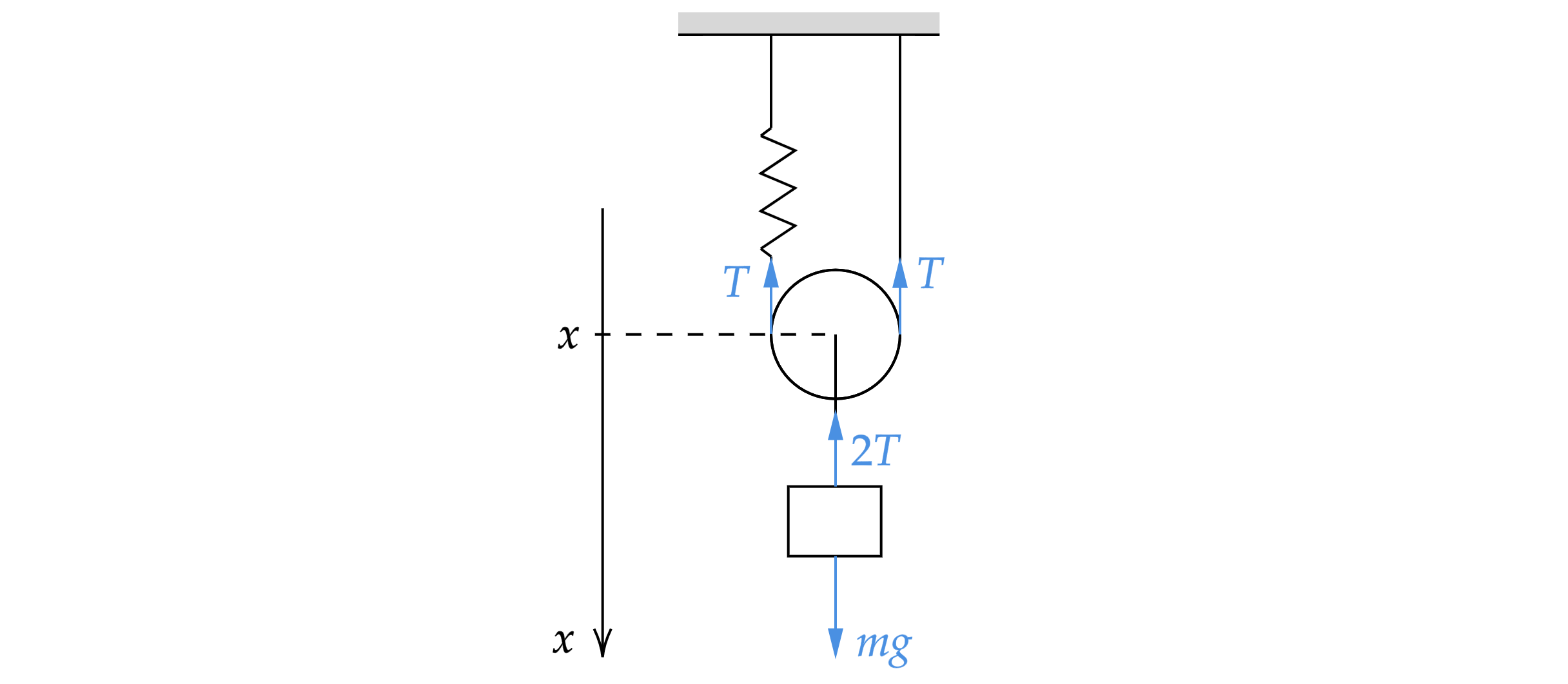
По второму закону Ньютона для груза
Длина нити и пружины равны:
продифференцируем по времени дважды:
С учетом второго закона Ньютона:
Получили уравнение гармонических колебаний с циклической частотой
Тогда период
| Критерии оценивания выполнения задачи | Баллы |
| Записана формула силы упргости пружины | 2 |
| Записан второй закон Ньютона | 2 |
| Записана деформация пружины | 2 |
| Записана формула периода гармонических колебаний | 2 |
| Представлен правильный ответ | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




