.02 Колебательные системы
Ошибка.
Попробуйте повторить позже
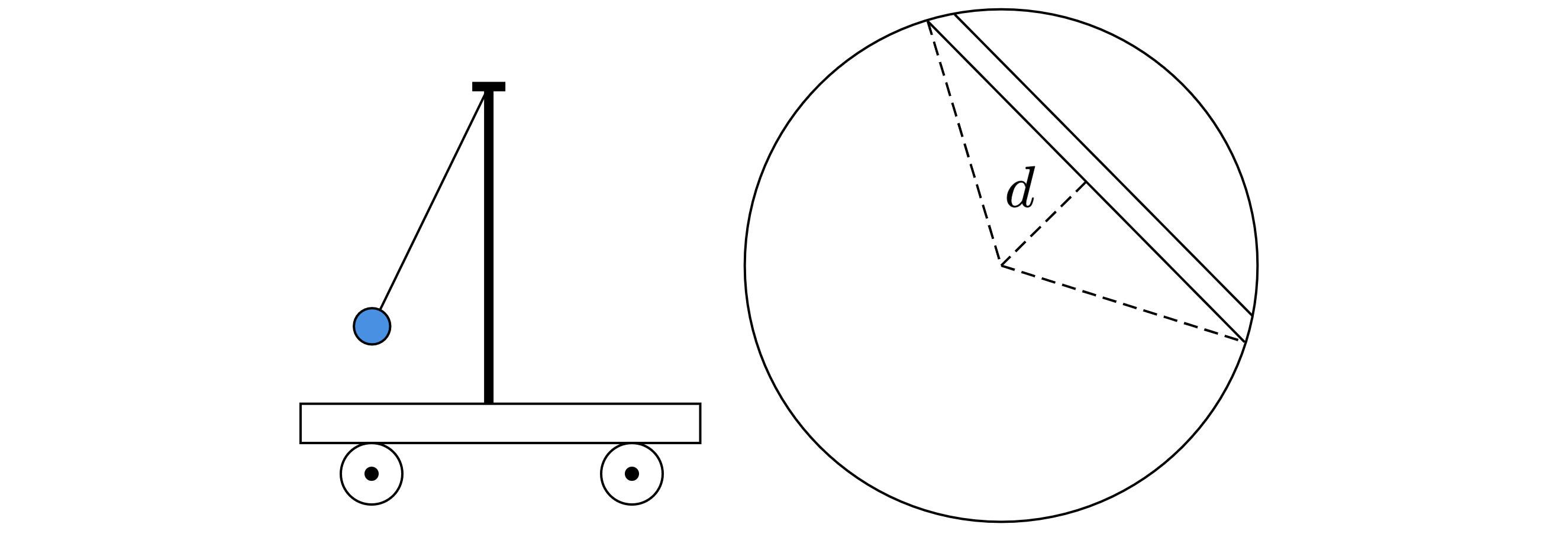
На тележке укреплен математический маятник длины . Тележку отпускают в туннель, прокопанный
внутри Земли по такой хорде, что минимальное расстояние от центра Земли до туннеля равно половине
радиуса Земли:
(
– радиус Земли; см. рисунок). Сколько колебаний совершит маятник за то
время, когда тележка пройдет весь туннель? Радиус и масса Земли
и ускорение свободного падения на
поверхности Земли известны. Плоскость колебаний маятника совпадает с направлением движения тележки.
(«Росатом», 2020, 11)
Источники:
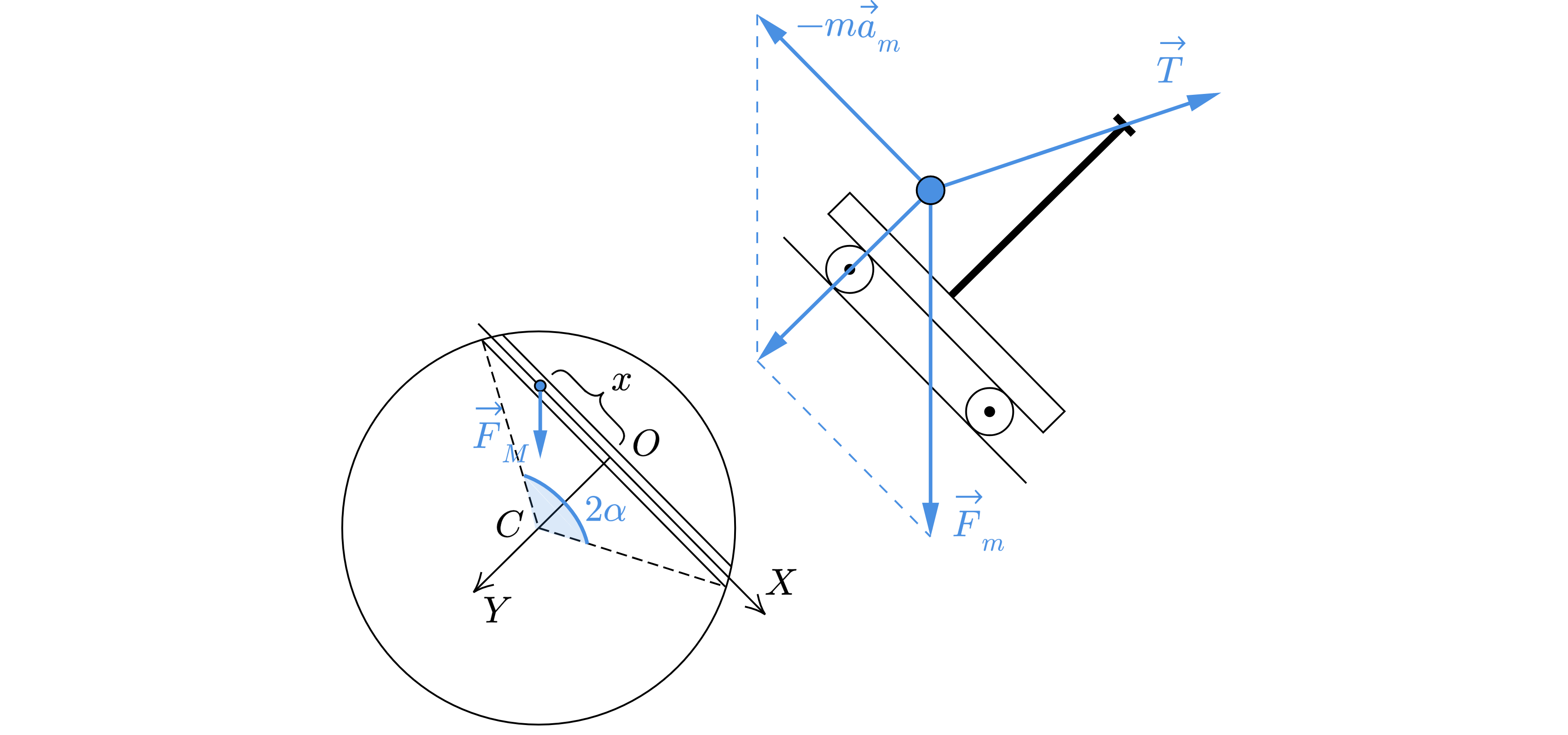
Пусть туннель «опирается» на угол (см. рисунок). Как известно, на тело массой
, находящееся внутри Земли на
расстоянии
от ее центра, действует направленная к центру Земли сила тяжести
где – сила тяжести, действующая на тело на поверхности Земли,
– радиус Земли. Применяя второй закон
Ньютона к тележке, найдем, что ее ускорение
направлено вдоль туннеля и равно по величине
где – проекция силы тяжести на ось OX, направленную вдоль туннеля (см. рисунок),
– масса тележки.
Поскольку
, из уравнения (1) следует
что ускорение тележки пропорционально расстоянию от нее до точки (ближайшей к центру точки туннеля); это
значит, что тележка (вместе с маятником на ней) будет совершать гармонические колебания относительно точки
с
периодом
Следовательно, до противоположной точки туннеля тележка доедет за половину периода
(причем независимо от того, на какой угол «опирается» туннель). Второй закон Ньютона для маятника имеет вид
где масса маятника,
– его ускорение в инерциальной системе отсчета (например, относительно Земли),
–
сила натяжения нити. Но поскольку маятник колеблется на тележке, которая движется с ускорением, нам нужно найти
его ускорение относительно тележки
. Используя далее, закон, аналогичный закону сложения скоростей (но для
ускорений)
, получим
(для знакомых с понятием сил инерции отметим, что уравнение (4) является вторым законом Ньютона в
неинерциальной системе отсчета, связанной с тележкой, а и есть действующая на маятник сила инерции). Но с
учетом (1) величина
есть проекция действующей на маятник силы тяжести на ось
, поэтому вектор
направлен перпендикулярно туннелю, а его величина равна проекции силы тяжести на ось OY , перпендикулярную
туннелю. Поэтому модуль этого вектора равен
и не меняется в процессе движения тележки по туннелю (см. рисунок). Из уравнений (4)–(5) следует, что уравнение для
ускорения маятника относительно тележки совпадает с уравнением для ускорения математического маятника, но в
качестве «силы тяжести» в нем фигурирует постоянная сила . А это значит, что маятник будет совершать
колебания с периодом
Поэтому за время (3) маятник совершит следующее количество колебаний
(Официальное решение Росатом)
| Критерии оценивания выполнения задачи | Баллы |
| Правильно найдена или использована сила тяжести, действующая на тележку внутри Земли | 0.5 |
| Доказано, что движение тележки по шахте представляет собой гармоническое колебание и правильно найден его период | 0.5 |
| Правильно найдено ускорение маятника относительно тележки | 0.5 |
| Правильный ответ | 0.5 |
| Максимальный балл | 2 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




