.02 Колебательные системы
Ошибка.
Попробуйте повторить позже
Горизонтально расположенная упругая пружина массой под действием силы, равной её весу
,
растягивается (или сжимается) на величину
.
1) Чему будет равно удлинение данной пружины, если её подвесить за один конец (без груза)?
2) Чему будет равен период колебаний груза массой , скреплённого с одним из концов данной
пружины, если второй конец пружины неподвижен, а груз скользит по гладкой горизонтальной
поверхности?
Деформация пружины во всех случаях мала по сравнению с длиной недеформированной пружины.
(Всеросс., 1997, финал, 11)
Источники:
Жёсткость данной пружины
Найдем жёсткость небольшого элемента этой пружины длиной
. Если пружина
растянута на величину
, то очевидно, что удлинение
элемента пружины длиной
равно
где – длина пружины, при этом упругая сила в любом сечении пружины равна
. С
другой стороны, деформация элемента пружины
может быть записана в виде
Приравняв два выражения дл , получим
1) Рассмотрим вертикально подвешенную пружины (см. рис.).
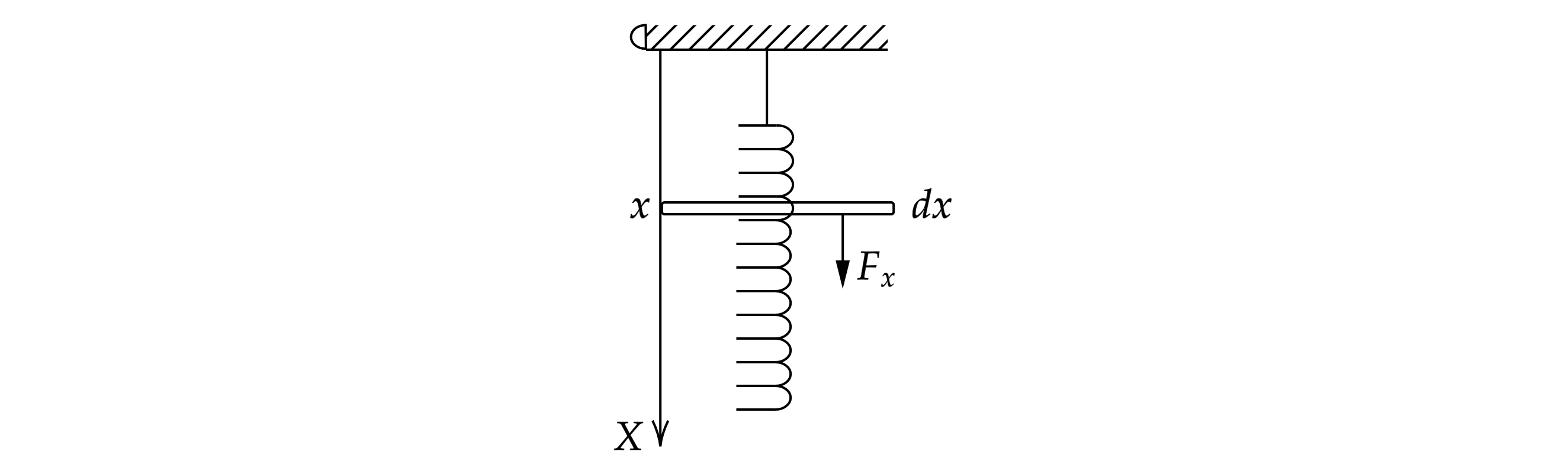
Распределение силы вдоль оси
будет иметь вид
Удлинение элемента пружины длиной , имеющего координату
, равно
Очевидно, что удлинение всей пружины
2) Пусть в некоторый момент времени груз массой сместился от равновесного положения
(
) на величину
(см. рис. 161).
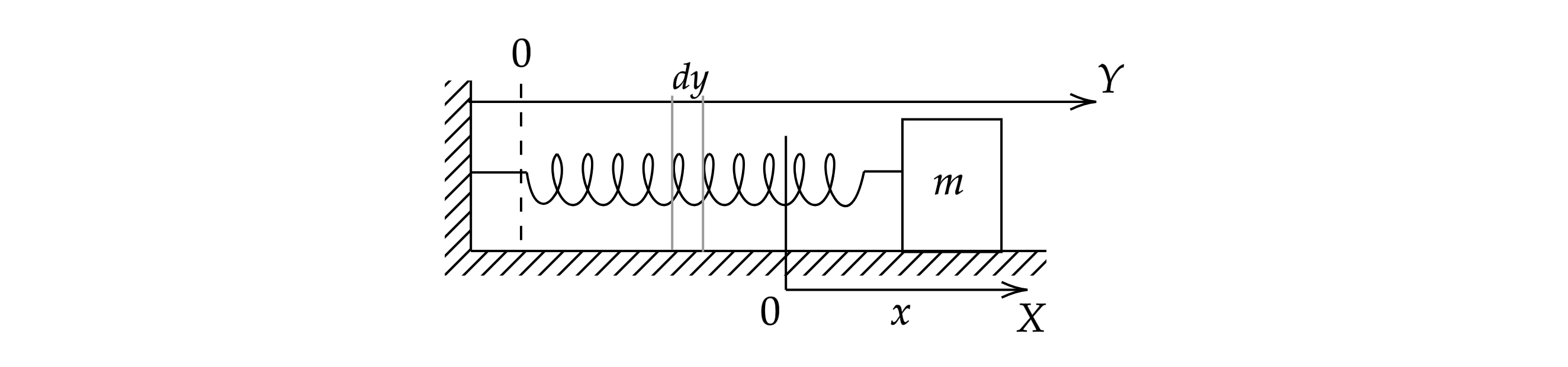
Найдем полную энергию системы "пружина + груз"массой . Кинетическая энергия
груза
Если смещение правого конца пружины , то смещение элемента пружины с координатой
равно
Следовательно, скорость элемента пружины с координатой
а кинетическая энергия элемента с длиной
Полная кинетическая энергия пружины
Теперь найдем энергию упругой деформации пружины
Полная энергия системы "пружина+груз"
Продифференцировав по времени , получим уравнение движения груза
Период колебания груза:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




